यदि \( \frac{5 + 2\sqrt{3}}{7 + 4\sqrt{3}} = a + b\sqrt{3} \) है, तो a और b का मान ज्ञात कीजिए।
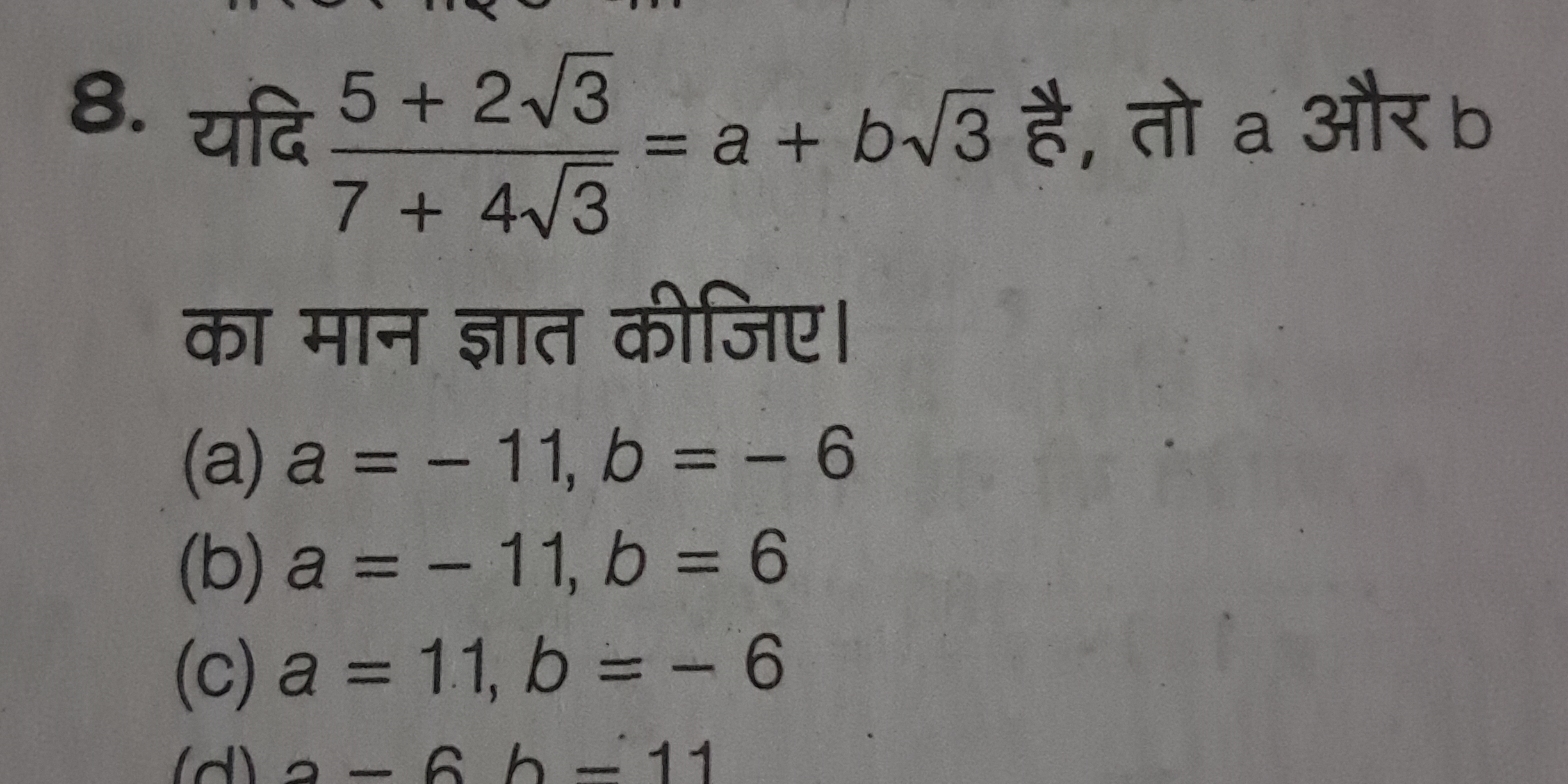
Understand the Problem
यह प्रश्न फractions और square roots से संबंधित है। हमें दिए गए fraction को a और b के रूप में निष्कर्षित करना है। हमें यह पता लगाना है कि a और b के मान क्या होंगे।
Answer
$a = 11$, $b = -6$
Answer for screen readers
$a = 11$, $b = -6$
Steps to Solve
- गुणनफल से सरल करना पहले हम पहले भुजाओं (5 + 2\sqrt{3}) और (7 + 4\sqrt{3}) के गुणनफल के लिए उसे समतल (rationalize) करेंगे। इसके लिये हम बहु श्रेणी (7 - 4\sqrt{3}) से गुणा करेंगे।
$$ \frac{(5 + 2\sqrt{3})(7 - 4\sqrt{3})}{(7 + 4\sqrt{3})(7 - 4\sqrt{3})} $$
- विश्लेषण करना गुणनफल का परिणाम निकालें। भुजा:
$$ (5 \times 7) + (5 \times -4\sqrt{3}) + (2\sqrt{3} \times 7) + (2\sqrt{3} \times -4\sqrt{3}) $$
यह होगा:
$$ 35 - 20\sqrt{3} + 14\sqrt{3} - 24 $$
- सरलीकरण अब हमको इसी परिणाम में भाग के व्यंजक को सरल करना है।
$$ 35 - 24 + (-20 + 14)\sqrt{3} = 11 - 6\sqrt{3} $$
- कुल परिणाम का विश्लेषण अब हम इसे (7 + 4\sqrt{3}) के वर्ग के भाग में डालेंगे:
$$ \frac{11 - 6\sqrt{3}}{(7 + 4\sqrt{3})(7 - 4\sqrt{3})} $$
- ध्यान दें कि हर भाग का मूल्य क्या है क्योंकि (7^2 - (4\sqrt{3})^2 = 49 - 48 = 1), इसलिए हम प्राप्त करते हैं:
$$ 11 - 6\sqrt{3} $$
अब इसे (a + b\sqrt{3}) के रूप में पारिभाषित कर सकते हैं: (a = 11) और (b = -6)।
$a = 11$, $b = -6$
More Information
यह उत्तर इस प्रकार व्यक्त किया गया है कि ( a ) और ( b ) की पहचान स्पष्ट हो जाये।
Tips
- अक्सर भाग को सरल करते समय गुणनफल की भी भुला देता है, जिससे गलत उत्तर प्राप्त होता है।
- अतिरिक्त मूल्यों का ध्यान नहीं रखना भी गलतियों का कारण बनता है।
AI-generated content may contain errors. Please verify critical information