∫ 1 / (x√(x² - a²)) dx = (1/a) sec^-1(x/a) + c
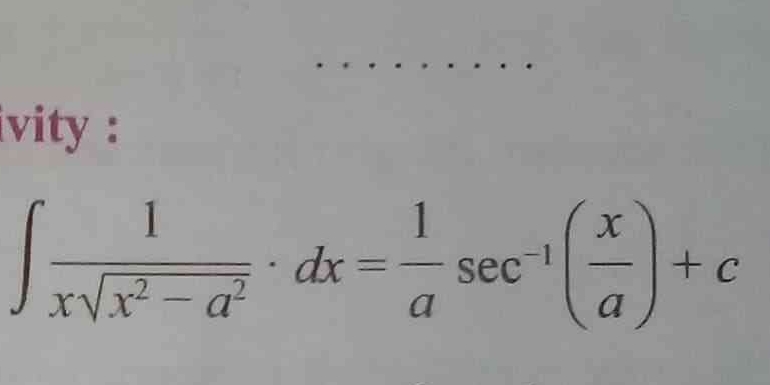
Understand the Problem
The question presents an integral equation that relates to calculus, specifically involving integration techniques. It demonstrates how an integral can be solved and states the result in terms of a known function, the inverse secant function.
Answer
The integral evaluates to $$ \int \frac{1}{x\sqrt{x^2 - a^2}} \, dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
Answer for screen readers
The solution to the integral is
$$ \int \frac{1}{x\sqrt{x^2 - a^2}} , dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
Steps to Solve
- Identify the Integral Form The given integral is
$$ \int \frac{1}{x\sqrt{x^2 - a^2}} , dx $$
which can be solved using trigonometric substitution or known integral formulas.
- Recognize the Form of the Integral This integral resembles the derivative of the inverse secant function, given by
$$ \frac{d}{dx} \sec^{-1}\left(\frac{x}{a}\right) = \frac{1}{|x| \sqrt{x^2 - a^2}} $$
Thus, we will use this relationship in our solution.
- Rewrite the Integral Using Known Results We can rewrite the integral based on the relationship identified with the inverse secant function:
$$ \int \frac{1}{x\sqrt{x^2 - a^2}} , dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
- Add the Constant of Integration Don’t forget to add the constant of integration ( C ) to the result.
The solution to the integral is
$$ \int \frac{1}{x\sqrt{x^2 - a^2}} , dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
More Information
This integral is particularly useful in calculus and can arise in various applications, including physics and engineering. The inverse secant function is the antiderivative related to this integral, providing a geometric interpretation.
Tips
- Forgetting the absolute value in the derivative of the inverse secant function, which leads to incorrect signs in the final answer.
- Neglecting to add the constant of integration ( C ).
AI-generated content may contain errors. Please verify critical information