y = -1 / (5 + x)
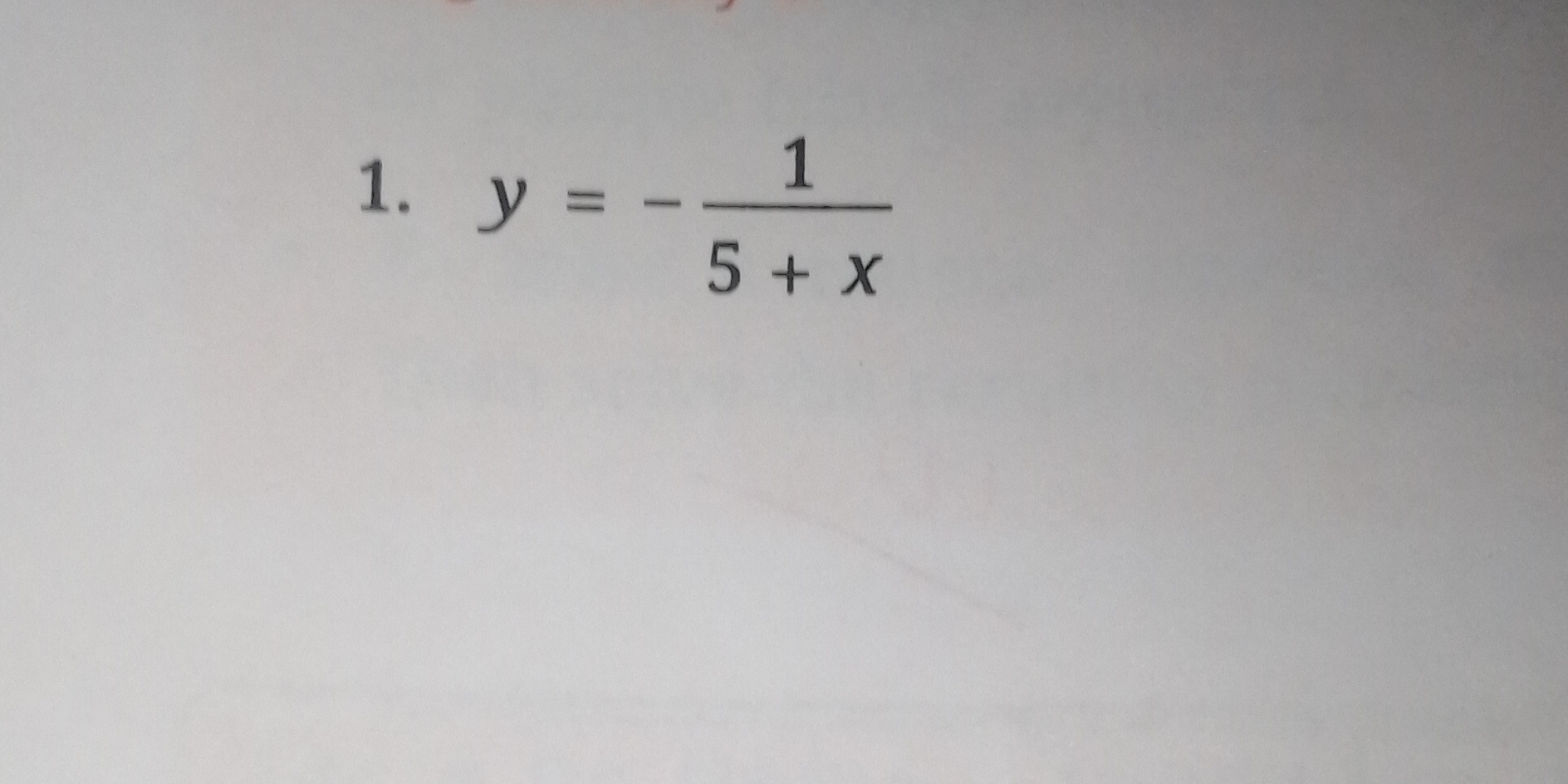
Understand the Problem
The question presents a mathematical equation involving y and x, specifically saying that y equals negative one divided by the expression '5 + x'. It seems to seek further exploration or manipulation of this equation, likely requiring a mathematical solution or simplification.
Answer
The expression for $x$ in terms of $y$ is $$ x = -\frac{1}{y} - 5 $$
Answer for screen readers
The expression for $x$ in terms of $y$ is
$$ x = -\frac{1}{y} - 5 $$
Steps to Solve
- Identify the equation
The equation given is:
$$ y = -\frac{1}{5 + x} $$
- Rewrite for better understanding
Let’s express the equation more readable for potential manipulations.
We can multiply both sides by $(5 + x)$ (assuming $5 + x \neq 0$):
$$ y(5 + x) = -1 $$
- Isolate x
Now we will isolate $x$:
Distributing $y$ gives:
$$ 5y + xy = -1 $$
Now, rearranging to isolate $x$:
$$ xy = -1 - 5y $$
Dividing both sides by $y$ (assuming $y \neq 0$) gives:
$$ x = \frac{-1 - 5y}{y} $$
- Final expression
So the expression for $x$ in terms of $y$ is:
$$ x = -\frac{1}{y} - 5 $$
The expression for $x$ in terms of $y$ is
$$ x = -\frac{1}{y} - 5 $$
More Information
This equation shows how $x$ is dependent on $y$. It also emphasizes the relationship between the two variables, which is useful in understanding their behavior in different contexts, such as graphing.
Tips
- Misinterpreting the equation: Ensure the signs are correct, as the negative affects the entire fraction.
- Forgetting to consider the cases where $y = 0$ or $5 + x = 0$, which leads to undefined situations.
AI-generated content may contain errors. Please verify critical information