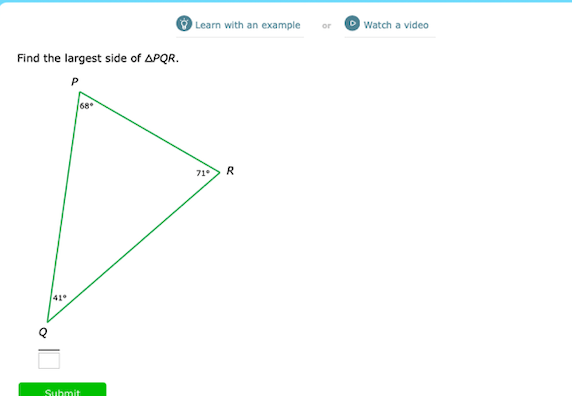
Find the largest side of triangle PQR.

Understand the Problem

The question is asking for the identification of the largest side of triangle PQR based on the given angles. To find this, we will use the property that the largest side is opposite the largest angle.

Answer

The largest side of triangle PQR is side $PQ$.

Steps to Solve

Identify the given angles The angles of triangle PQR are:

$P = 68^\circ$
$Q = 41^\circ$
$R = 71^\circ$

Determine the largest angle To find the largest angle, compare the three given angles:

$P = 68^\circ$
$Q = 41^\circ$
$R = 71^\circ$

The largest angle is $R = 71^\circ$.

Identify the corresponding side The side opposite the largest angle ($R$) is side $PQ$. Therefore, $PQ$ is the largest side of triangle PQR.

The largest side of triangle PQR is side $PQ$.

More Information

In any triangle, the side opposite the largest angle is the longest side. This concept is an important property in triangle geometry, often referred to as the "Triangle Inequality Theorem."

Tips

Confusing angle measures for side lengths; always remember the relationship that the largest angle corresponds to the longest side.
Miscalculating the angles; ensure to check that the angles indeed add up to $180^\circ$.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!