x^2 \frac{dy}{dx} + y^2 = xy
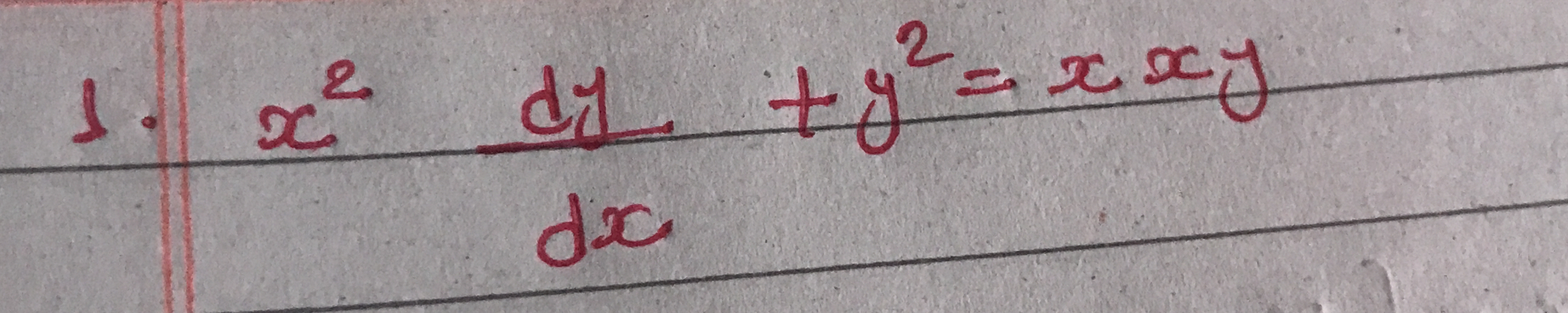
Understand the Problem
The question expresses a mathematical equation involving derivatives and variables, specifically how to manipulate or solve the given differential equation. The equation presented is related to calculus.
Answer
The solution involves relations of the form: $$ A \ln |y| - B \ln |x - y| = -\frac{1}{x} + C $$ Where \(A\), \(B\), and \(C\) are constants.
Answer for screen readers
The general solution of the differential equation is represented by a relation of the form:
$$ A \ln |y| - B \ln |x - y| = -\frac{1}{x} + C $$
Where (A), (B), and (C) are constants determined by initial conditions.
Steps to Solve
-
Rearrange the Differential Equation
We start with the given equation:
$$ x^2 \frac{dy}{dx} + y^2 = xy $$
Rearranging it yields:
$$ x^2 \frac{dy}{dx} = xy - y^2 $$ -
Factor out (y)
On the right-hand side, we can factor (y):
$$ x^2 \frac{dy}{dx} = y(x - y) $$ -
Separate Variables
Now, we'll separate the variables (y) and (x):
$$ \frac{dy}{y(x - y)} = \frac{dx}{x^2} $$ -
Integrate Both Sides
Next, integrate both sides:
- Left-hand side:
$$ \int \frac{dy}{y(x - y)} $$ - Right-hand side:
$$ \int \frac{dx}{x^2} $$
We can rewrite the right side as:
$$ \int x^{-2} dx = -\frac{1}{x} + C_1 $$ - Left-hand side:
-
Solve the Left Side Integral (Using Partial Fractions)
The left-hand side integral can be solved using partial fractions:
$$ \frac{1}{y(x - y)} = \frac{A}{y} + \frac{B}{x - y} $$After integrating, we obtain:
$$ A \ln |y| - B \ln |x - y| = -\frac{1}{x} + C_1 $$ -
Combine and Rearrange
Finally, combine and solve for (y) in terms of (x). This will involve exponentiation and may require simplification based on the constants.
The general solution of the differential equation is represented by a relation of the form:
$$ A \ln |y| - B \ln |x - y| = -\frac{1}{x} + C $$
Where (A), (B), and (C) are constants determined by initial conditions.
More Information
This differential equation is a first-order equation that can be solved using separation of variables and partial fractions. Such equations frequently appear in calculus and various applications in physics and engineering.
Tips
- Confusing the steps of integration: Ensure that you correctly identify when to use partial fractions.
- Failing to separate variables properly: Double-check that variables (y) and (x) are isolated on their respective sides.
- Not simplifying the final equation: Always look for simplification of the constants or the relationship after integration.
AI-generated content may contain errors. Please verify critical information