Determine whether the following functions are even, odd, or neither algebraically.
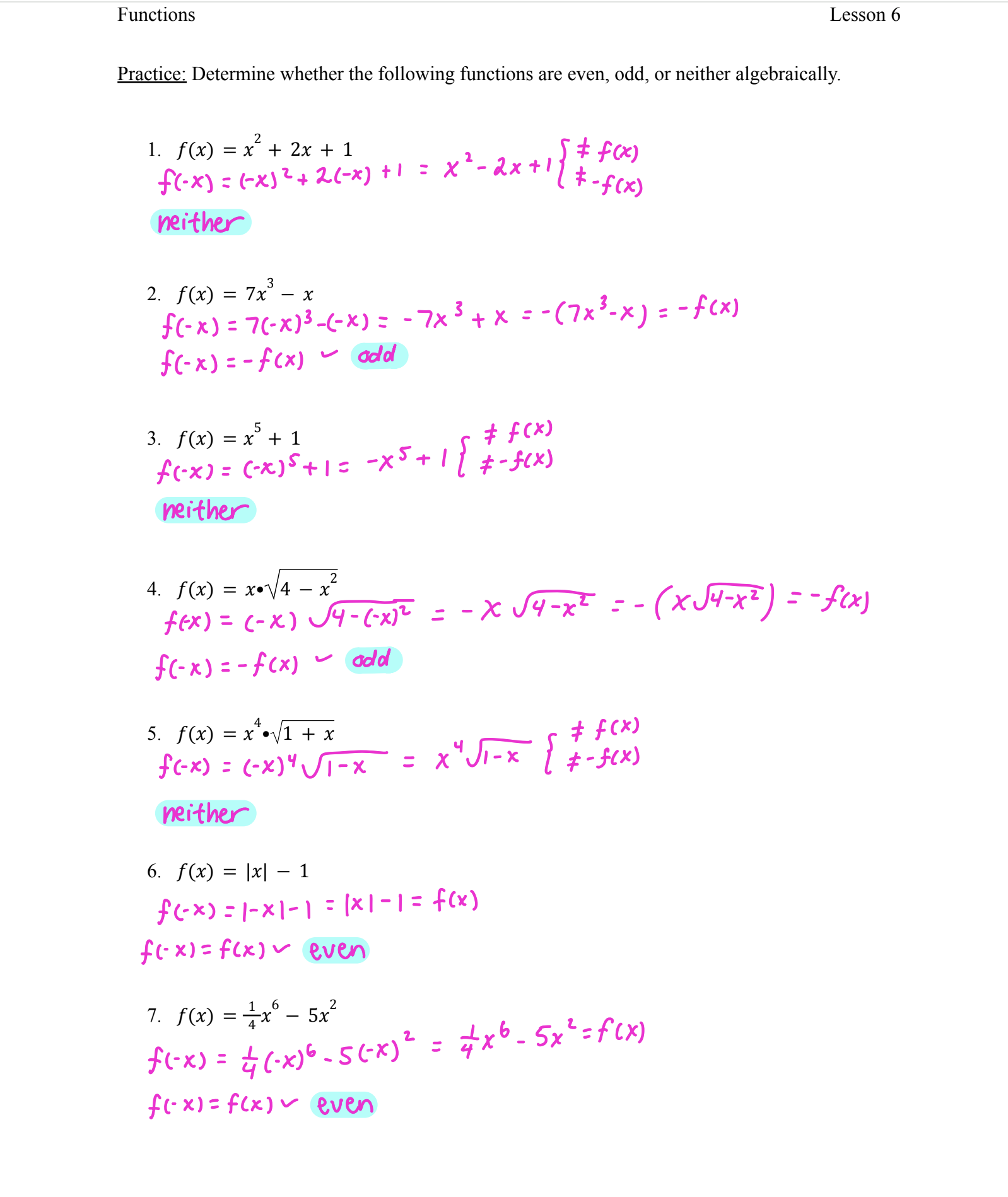
Understand the Problem
The question presents a series of functions and asks to determine whether each function is even, odd, or neither using algebraic methods. This involves evaluating the functions when the input variable is negated and checking the resulting expressions against the definitions of even and odd functions.
Answer
1. Neither 2. Odd 3. Neither 4. Odd 5. Neither 6. Even 7. Even
Answer for screen readers
- Neither
- Odd
- Neither
- Odd
- Neither
- Even
- Even
Steps to Solve
-
Evaluate ( f(-x) ) for each function
First, you'll need to substitute (-x) in place of (x) in each function and simplify. -
Check the definitions of even and odd
- Even: A function is even if ( f(-x) = f(x) ) for all ( x ).
- Odd: A function is odd if ( f(-x) = -f(x) ) for all ( x ).
- Neither: If it doesn't fit either condition, it's neither.
-
Function 1: ( f(x) = x^2 + 2x + 1 )
- ( f(-x) = (-x)^2 + 2(-x) + 1 = x^2 - 2x + 1 )
- Compare: ( f(-x) \neq f(x) ) and ( f(-x) \neq -f(x) )
-
Function 2: ( f(x) = 7x^3 - x )
- ( f(-x) = 7(-x)^3 - (-x) = -7x^3 + x )
- Compare: ( f(-x) = -f(x) )
-
Function 3: ( f(x) = x^5 + 1 )
- ( f(-x) = (-x)^5 + 1 = -x^5 + 1 )
- Compare: ( f(-x) \neq f(x) ) and ( f(-x) \neq -f(x) )
-
Function 4: ( f(x) = x \sqrt{4 - x^2} )
- ( f(-x) = -x \sqrt{4 - (-x)^2} = -x \sqrt{4 - x^2} )
- Compare: ( f(-x) = -f(x) )
-
Function 5: ( f(x) = x^4 \sqrt{1 - x} + x )
- ( f(-x) = (-x)^4 \sqrt{1 - (-x)} + (-x) = x^4 \sqrt{1 + x} - x )
- Compare: ( f(-x) \neq f(x) ) and ( f(-x) \neq -f(x) )
-
Function 6: ( f(x) = |x| - 1 )
- ( f(-x) = |-x| - 1 = |x| - 1 )
- Compare: ( f(-x) = f(x) )
-
Function 7: ( f(x) = \frac{1}{4}x^6 - 5x^2 )
- ( f(-x) = \frac{1}{4}(-x)^6 - 5(-x)^2 = \frac{1}{4}x^6 - 5x^2 )
- Compare: ( f(-x) = f(x) )
- Neither
- Odd
- Neither
- Odd
- Neither
- Even
- Even
More Information
The classifications of functions as even or odd help understand their symmetry properties. Even functions are symmetric about the y-axis, while odd functions are symmetric about the origin.
Tips
- Confusing the signs when substituting (-x) for (x).
- Misapplying the definitions of even and odd functions, especially when simplifying the expressions.
AI-generated content may contain errors. Please verify critical information