∫ (x^2 + 4x^3 + 2) / (6x) dx
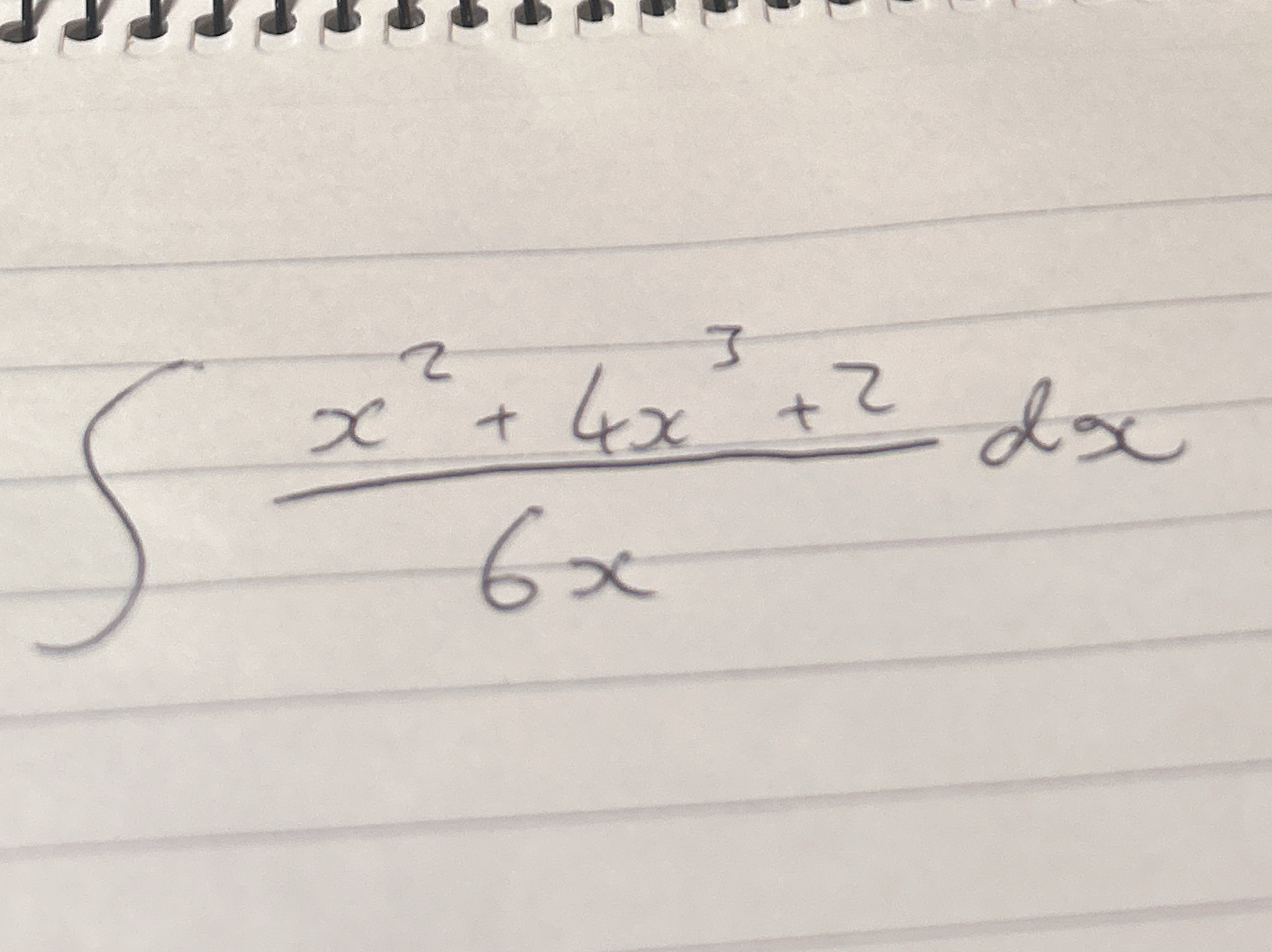
Understand the Problem
The question asks for the evaluation of a definite integral involving the polynomial fraction (x^2 + 4x^3 + 2) / (6x). This indicates a mathematical problem requiring integration techniques.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
Answer for screen readers
The final answer to the integral is: $$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
Steps to Solve
-
Simplify the Integral To begin, we can divide each term in the polynomial by (6x): $$ \int \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} , dx $$ This simplifies to: $$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) , dx $$
-
Separate the Integral Next, we can separate the integrated terms: $$ \int \left( \frac{x}{6} \right) , dx + \int \left( \frac{2}{3}x^2 \right) , dx + \int \left( \frac{1}{3x} \right) , dx $$
-
Integrate Each Term Now, we will integrate each term individually:
- For the first term: $$ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
- For the second term: $$ \int \frac{2}{3}x^2 , dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2x^3}{9} $$
- For the third term: $$ \int \frac{1}{3x} , dx = \frac{1}{3} \ln|x| $$
- Combine the Results Now, we combine our integrated results: $$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
The final answer to the integral is: $$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
More Information
This integral represents the antiderivative of the function ( \frac{x^2 + 4x^3 + 2}{6x} ). The constant ( C ) is the integration constant, acknowledging that indefinite integrals can differ by a constant.
Tips
- Forgetting to simplify the fraction before integrating can lead to complex fractions that complicate the math unnecessarily.
- Omitting the constant ( C ) in indefinite integrals is a common error; always remember to include it.
AI-generated content may contain errors. Please verify critical information