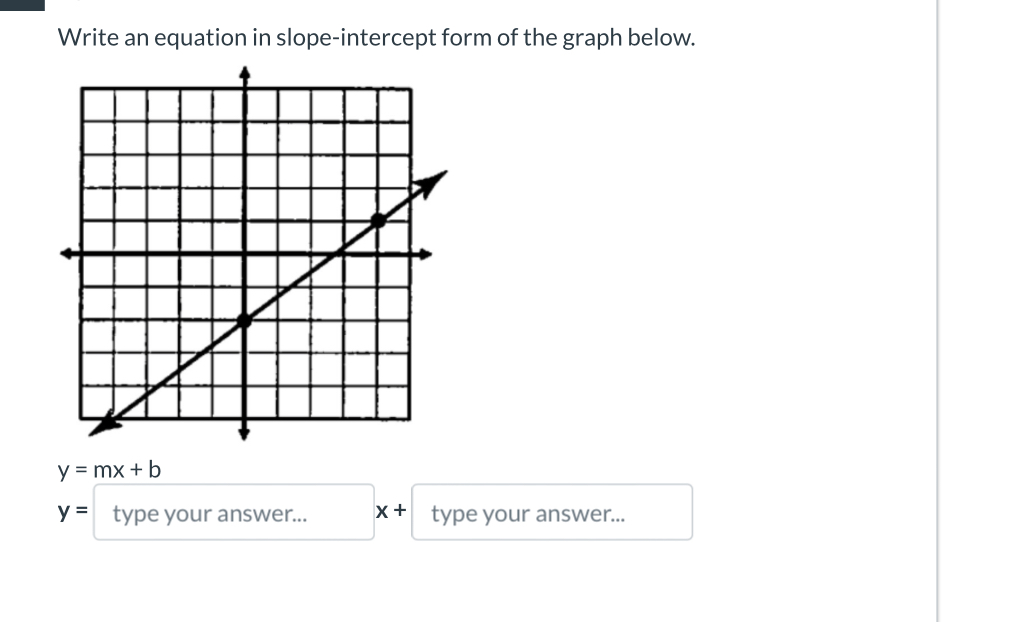
Write an equation in slope-intercept form of the graph below.
Understand the Problem
The question is asking to write the equation of a line in slope-intercept form (y = mx + b) based on the graph provided. This involves determining the slope (m) and the y-intercept (b) from the graph.
Answer
The equation of the line is $y = x + 2$.
Answer for screen readers
The equation of the line in slope-intercept form is:
$$ y = x + 2 $$
Steps to Solve
-
Identify the y-intercept (b) Look at where the line crosses the y-axis. From the graph, the line crosses at (0, 2).
Thus, $b = 2$.
-
Determine the slope (m) To find the slope, use two points on the line. Let's take the points (0, 2) and (2, 4).
The slope formula is: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$ Substituting the points: $$ m = \frac{4 - 2}{2 - 0} = \frac{2}{2} = 1 $$
-
Write the equation in slope-intercept form Now, we can plug the slope ($m=1$) and the y-intercept ($b=2$) into the slope-intercept form of the equation $y = mx + b$:
Thus, the equation is: $$ y = 1x + 2 $$
-
Simplify the equation Since 1 is the coefficient of $x$, we can simplify it to:
$$ y = x + 2 $$
The equation of the line in slope-intercept form is:
$$ y = x + 2 $$
More Information
The slope-intercept form of a linear equation allows you to easily identify the slope and y-intercept. The slope of 1 indicates that for every unit you move right along the x-axis, the line rises by 1 unit on the y-axis.
Tips
- Mistaking the direction of the slope: Ensure you calculate the increase or decrease correctly using consistent points on the line.
- Using the wrong points to calculate slope: Always pick points that are clearly on the line to avoid errors.
AI-generated content may contain errors. Please verify critical information