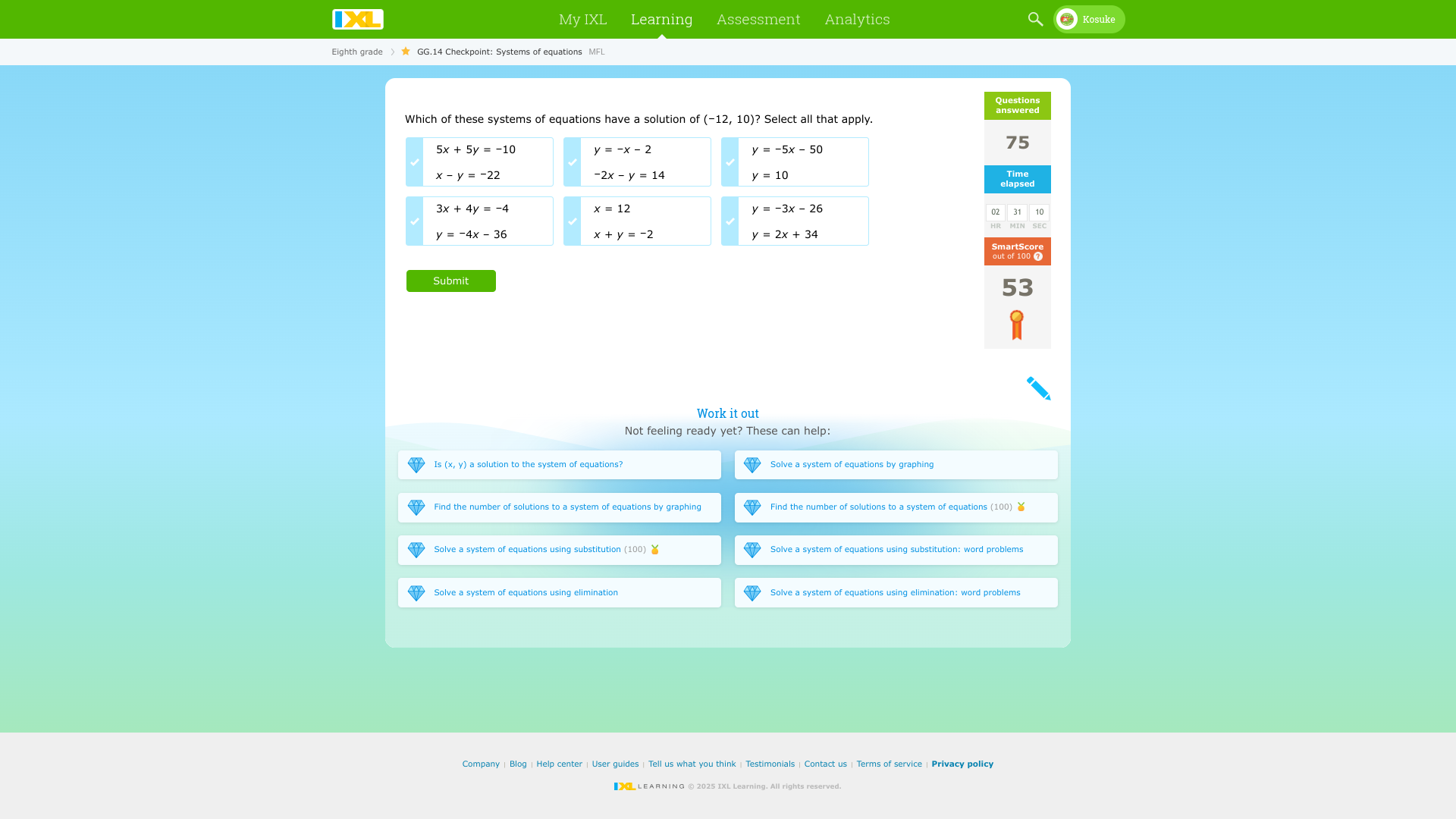
Which of these systems of equations have a solution of (-12, 10)? Select all that apply.

Steps to Solve

1. Substituting in the first system

   For the first system: [ \begin{align*} 5x + 5y &= -10 \ x - y &= -22 \end{align*} ] Substitute $x = -12$ and $y = 10$ into both equations: [ 5(-12) + 5(10) = -10 \quad \text{(Check if this is true)} ] [ -12 - 10 = -22 ] Both equations hold true.

2. Substituting in the second system

   For the second system: [ \begin{align*} y &= -x - 2 \ y &= -5x - 50 \end{align*} ] Substitute $x = -12$ and $y = 10$: [ 10 = -(-12) - 2 \quad \text{and} \quad 10 = -5(-12) - 50 ] Check if both equations are valid.

3. Substituting in the third system

   For the third system: [ \begin{align*} 3x + 4y &= -4 \ y &= -4x - 36 \end{align*} ] Substitute $x = -12$ and $y = 10$: [ 3(-12) + 4(10) = -4 \quad \text{and} \quad 10 = -4(-12) - 36 ] Check if both equations are valid.

4. Substituting in the fourth system

   For the fourth system: [ \begin{align*} x &= 12 \ x + y &= -2 \end{align*} ] Substitute $x = -12$ and $y = 10$: [ -12 = 12 \quad \text{and} \quad -12 + 10 = -2 ] Check the validity of both equations.

5. Substituting in the fifth system

   For the fifth system: [ \begin{align*} y &= -3x - 26 \ y &= 2x + 34 \end{align*} ] Substitute $x = -12$ and $y = 10$: [ 10 = -3(-12) - 26 \quad \text{and} \quad 10 = 2(-12) + 34 ] Check both equations for validity.