Solve using substitution: -5x + 6y = 2; x = 8
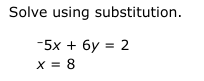
Understand the Problem
The question is asking to solve a system of equations using the substitution method. We have one equation in two variables and an already defined value for one variable (x = 8), which will be substituted into the other equation to find the value of y.
Answer
The values are \( x = 8 \) and \( y = 7 \).
Answer for screen readers
The solution to the system of equations is ( x = 8 ) and ( y = 7 ).
Steps to Solve
- Substitute the value of ( x ) into the equation
We are given ( x = 8 ). Substitute this value into the equation ( -5x + 6y = 2 ):
$$ -5(8) + 6y = 2 $$
- Simplify the equation
Calculate the left side of the equation:
$$ -40 + 6y = 2 $$
- Isolate ( y )
Add 40 to both sides of the equation to isolate the term with ( y ):
$$ 6y = 2 + 40 $$
This simplifies to:
$$ 6y = 42 $$
- Solve for ( y )
Divide both sides by 6 to find ( y ):
$$ y = \frac{42}{6} $$
This gives us:
$$ y = 7 $$
The solution to the system of equations is ( x = 8 ) and ( y = 7 ).
More Information
In this problem, we used the substitution method, which is a common technique for solving systems of linear equations. By substituting the known value of ( x ) into the equation, we were able to find the corresponding value for ( y ).
Tips
- A common mistake is forgetting to substitute the value correctly or miscalculating during substitution. Always double-check your arithmetic.
- Another mistake is not isolating ( y ) properly. Ensure to follow algebraic rules closely.
AI-generated content may contain errors. Please verify critical information