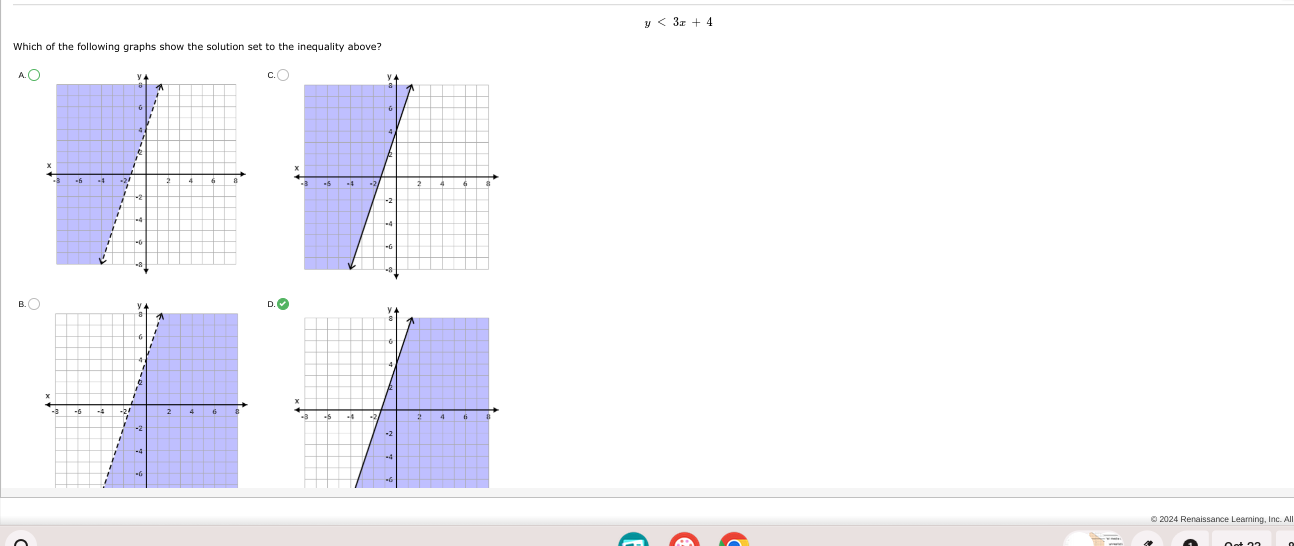
Which of the following graphs show the solution set to the inequality above?
Understand the Problem
The question is asking which of the provided graphs represents the solution set to the inequality y < 3x + 4. We need to identify between options A, B, C, and D, which graph shows the correct region shaded below the line 3x + 4, along with understanding whether the line is included or not (dashed since it is <).
Answer
The solution set for the inequality $y < 3x + 4$ is represented by graph **A**.
Answer for screen readers
The correct answer is option A.
Steps to Solve
- Identify the equation of the line
The given inequality is $y < 3x + 4$. The equation of the line that forms the boundary is $y = 3x + 4$.
- Determine the type of line
Since the inequality is "<" (not "≤"), the line will be dashed. This indicates that points on the line itself are not included in the solution set.
- Find the y-intercept and slope
From the equation $y = 3x + 4$, the y-intercept is 4, and the slope is 3. This means the line crosses the y-axis at the point (0, 4) and rises 3 units for every 1 unit it moves to the right.
- Shade the correct region
Since we are looking for the region where $y$ is less than $3x + 4$, we will shade the area below the dashed line.
- Analyze the graph options
Review the provided graphs (A, B, C, and D) to see which one correctly represents a dashed line that crosses through (0, 4) and shades the area below the line.
The correct answer is option A.
More Information
In the inequality $y < 3x + 4$, the area below the dashed line represents all points where the y-value is less than the corresponding points on the line $3x + 4$. The dashed line indicates that points on the line are not included in the solution.
Tips
- Confusing line types: Students might incorrectly use a solid line instead of a dashed line. Remember: "<" means the points on the line are not part of the solution.
- Incorrectly choosing the shading area: Ensuring you shade below the line for the "less than" inequality is crucial.
AI-generated content may contain errors. Please verify critical information