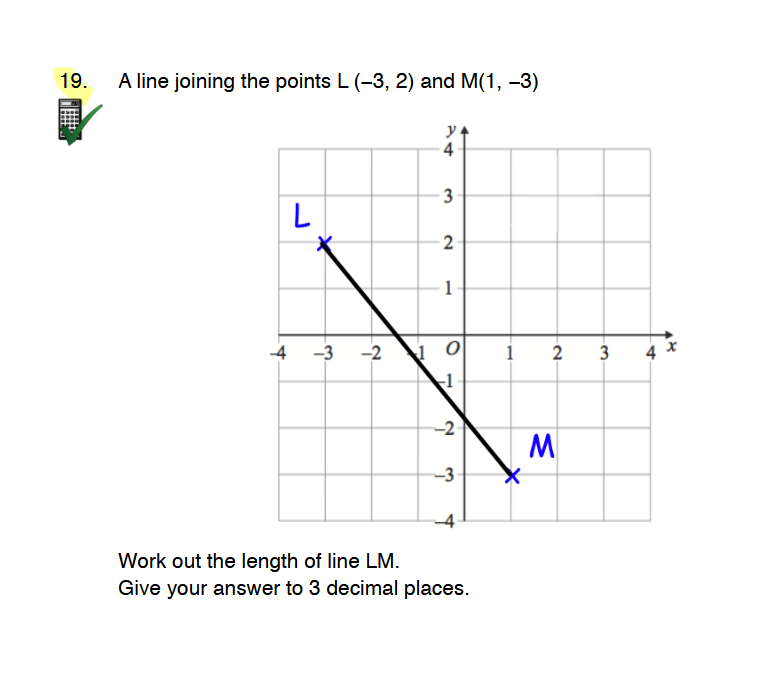
Work out the length of line LM. Give your answer to 3 decimal places.

Steps to Solve

1. Identify the coordinates of points L and M

The coordinates are given as follows:

• Point L: $(-3, 2)$
• Point M: $(1, -3)$

2. Use the distance formula

The distance (d) between two points ((x_1, y_1)) and ((x_2, y_2)) is calculated using the formula:

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

3. Plug in the coordinates into the formula

Substituting the coordinates for L and M into the formula:

• For L: ( x_1 = -3, y_1 = 2 )
• For M: ( x_2 = 1, y_2 = -3 )

This gives:

$$ d = \sqrt{(1 - (-3))^2 + (-3 - 2)^2} $$

4. Calculate the differences

Calculate (x_2 - x_1) and (y_2 - y_1):

• ( x_2 - x_1 = 1 + 3 = 4 )
• ( y_2 - y_1 = -3 - 2 = -5 )

5. Substitute the differences back into the distance formula

Now, substitute these differences back into the formula:

$$ d = \sqrt{(4)^2 + (-5)^2} $$

6. Calculate the squares and sum them

Calculating the squares:

$$ d = \sqrt{16 + 25} $$

$$ d = \sqrt{41} $$

7. Calculate the square root

Now we find the square root:

$$ d \approx 6.403 $$

8. Round to three decimal places

Therefore, rounding to three decimal places gives:

$$ d \approx 6.403 $$