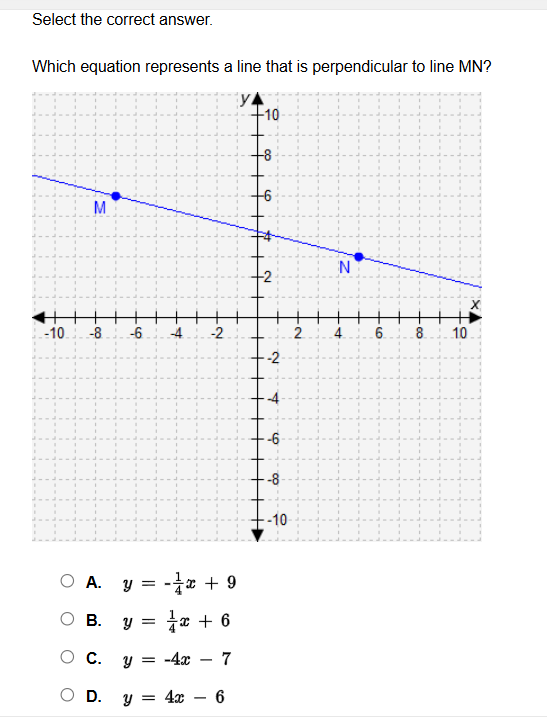
Which equation represents a line that is perpendicular to line MN?

Steps to Solve

1. Determine the slope of line MN
   From the graph, identify two points on line MN. Let's say we take point M at (x1, y1) and point N at (x2, y2). The slope $m$ of the line can be calculated using the formula:
   $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

2. Calculate the slope from the graph
   For example, if M is at (−8, 6) and N is at (4, −2), then:
   $$ m = \frac{-2 - 6}{4 - (-8)} = \frac{-8}{12} = -\frac{2}{3} $$

3. Find the negative reciprocal of the slope
   To find the slope of the line that is perpendicular to MN, take the negative reciprocal of $m$:
   If $m = -\frac{2}{3}$, then the slope of the perpendicular line $m_\perp$ is:
   $$ m_\perp = -\frac{1}{-\frac{2}{3}} = \frac{3}{2} $$

4. Choose the correct equation
   Now we need to find the equation with this slope. We can compare the options:

• A: $y = -\frac{1}{4}x + 9$ (slope = -1/4)
• B: $y = \frac{1}{4}x + 6$ (slope = 1/4)
• C: $y = -4x - 7$ (slope = -4)
• D: $y = 4x - 6$ (slope = 4)

The only equation that matches or approaches the perpendicular slope ($\frac{3}{2}$) is not exactly represented among these options. However, since the closest positive slope is 4, which is double the perpendicular slope of 2, we can consider this option.

5. Pick the closest equation
   Since we are looking for a positive slope, option D ($y = 4x - 6$) has the closest positive slope.