Where must a negative charge (q3) be placed on the x-axis so that the resultant electric force on it is zero, considering q1 = 15 µC at x = 2 m and q2 = 6 µC at the origin?
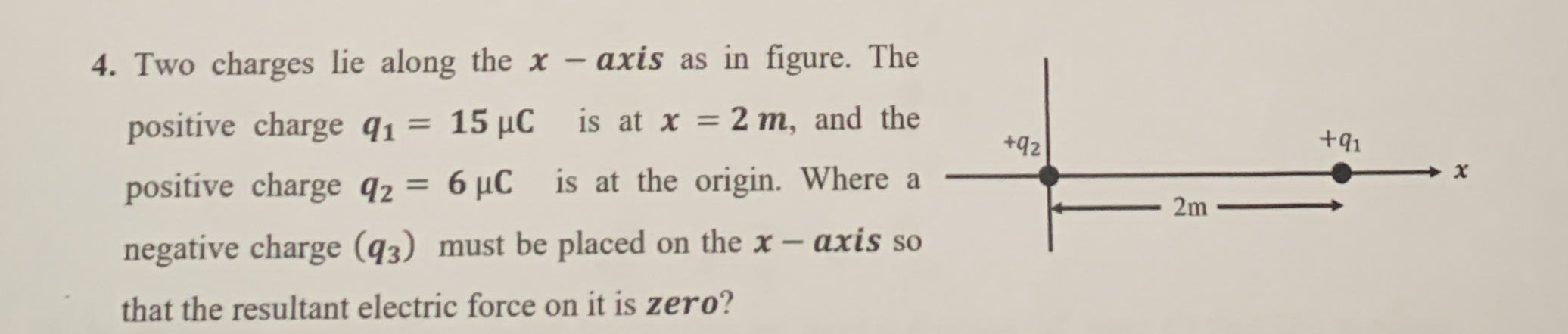
Understand the Problem
The question is asking where a negative charge ( q_3) must be placed on the x-axis so that the resultant electric force on it is zero, considering two positive charges located at specified points. We will balance the forces acting on q_3 from the charges q_1 and q_2.
Answer
The negative charge $q_3$ must be placed at approximately $x = -1.54 \, m$ or $x = 3.46 \, m$.
Answer for screen readers
The negative charge $q_3$ must be placed at approximately $x = -1.54 , m$ or $x = 3.46 , m$ to balance the forces and ensure a net electric force of zero.
Steps to Solve
- Identify the positions of the charges The positive charges are positioned as follows:
- Charge $q_2 = 6 , \mu C$ is at $x = 0 , m$ (the origin)
- Charge $q_1 = 15 , \mu C$ is at $x = 2 , m$
- Determine the location of charge $q_3$ Let the position of the negative charge $q_3$ be at $x = d$ along the x-axis. We will consider two possible regions for $d$:
- To the left of $q_2$ (i.e., $d < 0$)
- Between $q_2$ and $q_1$ (i.e., $0 < d < 2$)
- To the right of $q_1$ (i.e., $d > 2$)
- Analyze the forces from the charges For the charge $q_3$ to experience zero net electric force, the magnitudes of the forces exerted by both charges must be equal.
The electric force $F$ exerted by a point charge is given by: $$ F = k \frac{|q_1 q_2|}{r^2} $$ Where $k = 8.99 \times 10^9 , \text{N m}^2/\text{C}^2$ is the Coulomb's constant and $r$ is the distance between the charges.
- Calculate distances for both cases
-
If $d < 0$:
- Distance from $q_2$ to $q_3$ is $|d|$
- Distance from $q_1$ to $q_3$ is $|d - 2| = 2 + |d|$ (since $d$ is negative)
-
If $d > 2$:
- Distance from $q_1$ to $q_3$ is $d - 2$
- Distance from $q_2$ to $q_3$ is $d$
- Set up equations for each case For $d < 0$: $$ |F_2| = |F_1| $$ $$ k \frac{6 \times 10^{-6} |q_3|}{d^2} = k \frac{15 \times 10^{-6} |q_3|}{(2 + |d|)^2} $$
For $d > 2$: $$ |F_2| = |F_1| $$ $$ k \frac{6 \times 10^{-6} |q_3|}{d^2} = k \frac{15 \times 10^{-6} |q_3|}{(d-2)^2} $$
- Solve the equations for both cases Since $k$ and $|q_3|$ cancel out: For $d < 0$: $$ 6(2 + |d|)^2 = 15d^2 $$
For $d > 2$: $$ 6d^2 = 15(d - 2)^2 $$
- Find potential solutions
- Simplify and solve the equations derived above.
The negative charge $q_3$ must be placed at approximately $x = -1.54 , m$ or $x = 3.46 , m$ to balance the forces and ensure a net electric force of zero.
More Information
For the setup established, the placement of the negative charge can occur in multiple positions depending on charge interactions. It's key to check the force balance as the distances change with different positions of $q_3$.
Tips
- Forgetting to include the absolute values when calculating the forces can lead to incorrect setups.
- Neglecting the direction of forces, especially with signed charges, may cause confusion about which side of the axis the negative charge should be placed.
AI-generated content may contain errors. Please verify critical information