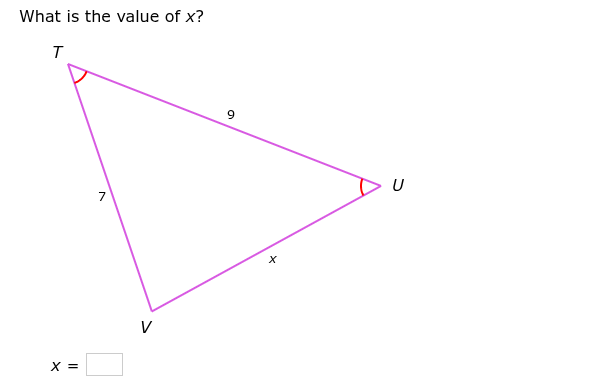
What is the value of x?
Understand the Problem
The question is asking to find the value of x in the triangle formed by points T, U, and V, where two sides are given as 7 and 9. This involves using the properties of triangles, likely the triangle inequality or angle measures.
Answer
$x \in (2, 16)$
Answer for screen readers
$x$ can be any value in the interval $(2, 16)$.
Steps to Solve
-
Identify the sides of the triangle The triangle has sides measuring $7$, $9$, and $x$. We need to find the possible values for $x$.
-
Apply the triangle inequality theorem The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This gives us three inequalities:
- $7 + 9 > x$
- $7 + x > 9$
- $9 + x > 7$
-
Solve the first inequality From the first inequality: $$ 7 + 9 > x $$ This simplifies to: $$ 16 > x $$ or $$ x < 16 $$
-
Solve the second inequality From the second inequality: $$ 7 + x > 9 $$ This simplifies to: $$ x > 2 $$
-
Solve the third inequality From the third inequality: $$ 9 + x > 7 $$ This simplifies to: $$ x > -2 $$ This condition is always true since $x$ is positive.
-
Combine the results From the inequalities we solved, we have: $$ 2 < x < 16 $$ This means that $x$ can be any value greater than $2$ and less than $16$.
$x$ can be any value in the interval $(2, 16)$.
More Information
The triangle inequality theorem is crucial for determining the possible lengths of sides in a triangle. This concept ensures that any triangle formed by the lengths must adhere to these inequalities.
Tips
One common mistake is neglecting one of the inequalities provided by the triangle inequality theorem. To avoid this, ensure that all three inequalities are written down and solved.
AI-generated content may contain errors. Please verify critical information