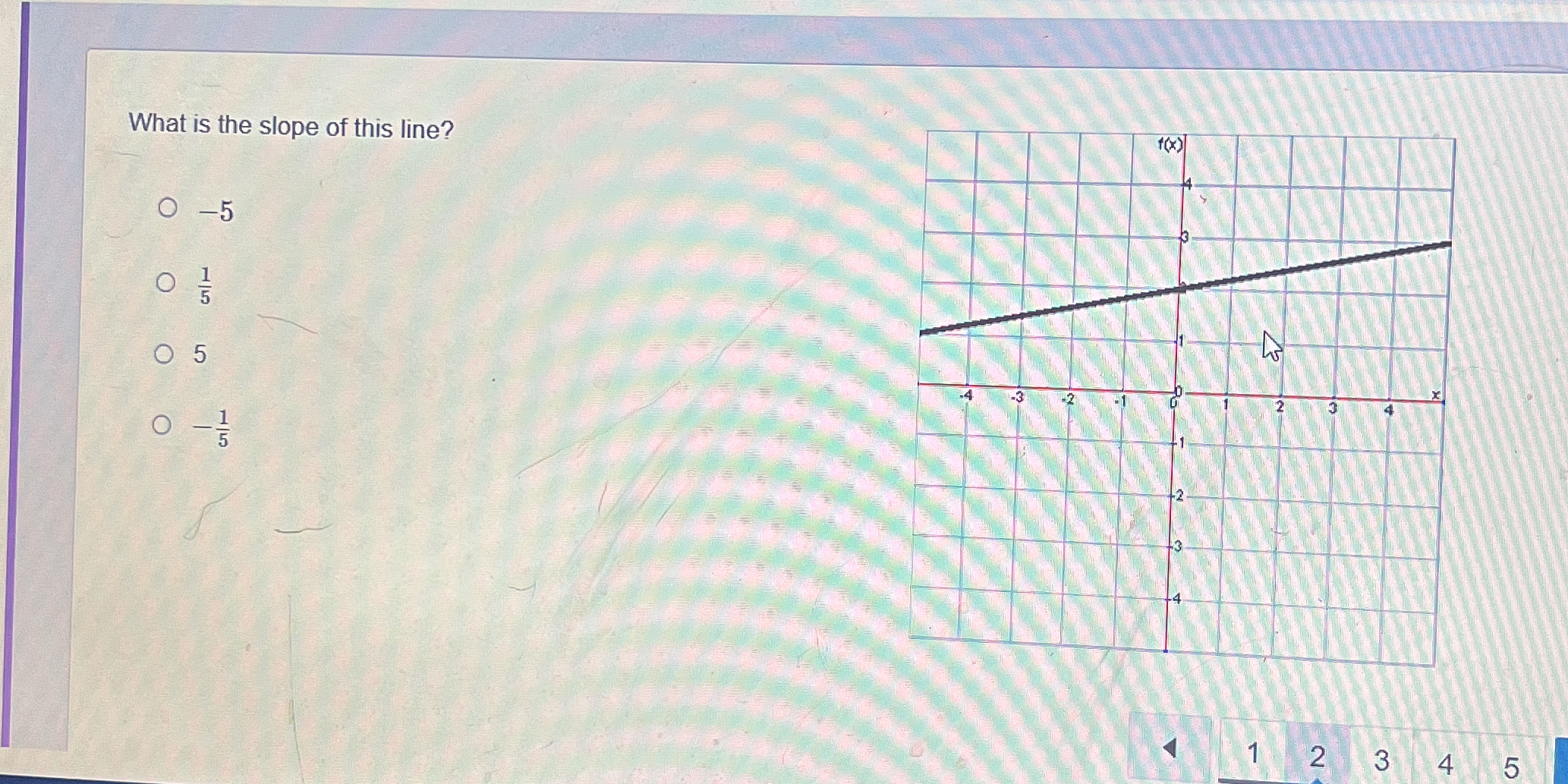
What is the slope of this line?
Understand the Problem
The question is asking for the slope of the line represented in the graph. To solve this, we need to identify two points on the line and then apply the slope formula, which is (change in y) / (change in x).
Answer
The slope of the line is \(1\).
Answer for screen readers
The slope of the line is (1).
Steps to Solve
- Identify Two Points on the Line
From the graph, we can select two easy-to-read points where the line intersects the grid. For example, let's choose point A at $(0, 1)$ and point B at $(1, 2)$.
- Calculate the Change in y and x
The change in $y$ (Δy) and change in $x$ (Δx) can be calculated as follows:
-
The change in $y$: $$ \Delta y = y_2 - y_1 = 2 - 1 = 1 $$
-
The change in $x$: $$ \Delta x = x_2 - x_1 = 1 - 0 = 1 $$
- Apply the Slope Formula
Now we can apply the slope formula, which is given by:
$$ m = \frac{\Delta y}{\Delta x} $$
Substituting our values into the formula:
$$ m = \frac{1}{1} = 1 $$
- Final Answer
Thus, the slope of the line is (1).
The slope of the line is (1).
More Information
The slope represents the steepness of the line. A slope of (1) means that for every unit increase in (x), (y) also increases by 1 unit, indicating a 45-degree angle with respect to the horizontal axis.
Tips
- Confusing the points; make sure to select accurate grid intersections.
- Miscalculating Δy or Δx due to not subtracting correctly.
AI-generated content may contain errors. Please verify critical information