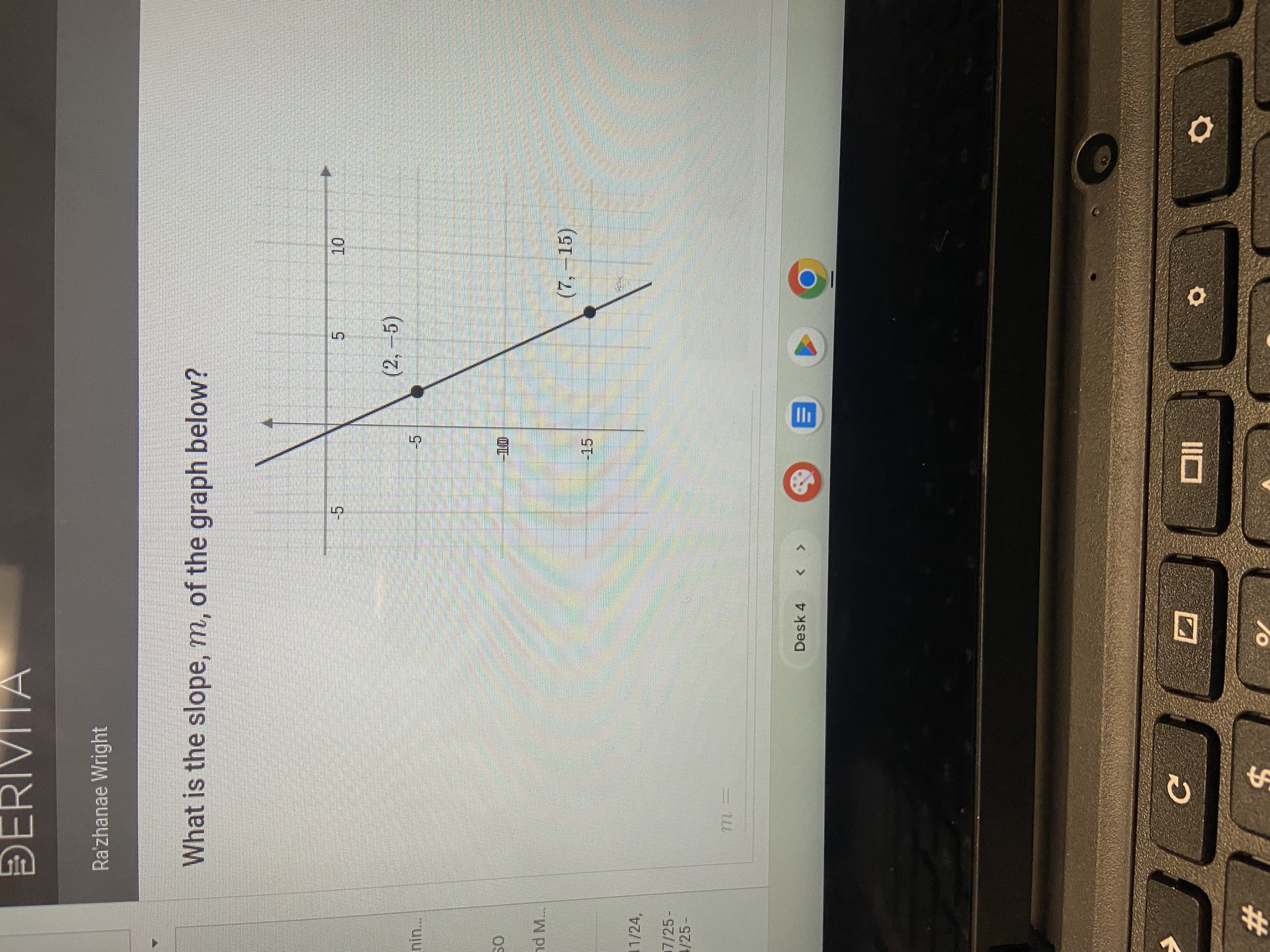
What is the slope, m, of the graph below?
Understand the Problem
The question is asking for the calculation of the slope (m) from a given graph that includes two points. This requires using the slope formula based on the coordinates of the points provided.
Answer
The slope is \( m = -2 \).
Answer for screen readers
The slope ( m ) of the graph is given by:
$$ m = -2 $$
Steps to Solve
- Identify the coordinates of the two points
From the graph, we have two points:
- Point 1: $(2, -5)$
- Point 2: $(7, -15)$
- Use the slope formula
The slope ( m ) between two points ((x_1, y_1)) and ((x_2, y_2)) is calculated using the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
In our case, substituting the coordinates into the formula, we have:
$$ m = \frac{-15 - (-5)}{7 - 2} $$
- Calculate the differences in the formula
Now calculate the differences in the formula:
-
For the numerator: $$ -15 - (-5) = -15 + 5 = -10 $$
-
For the denominator: $$ 7 - 2 = 5 $$
- Calculate the slope
Now, substitute the calculated values into the slope formula:
$$ m = \frac{-10}{5} $$
- Simplify the result
Finally, simplify:
$$ m = -2 $$
The slope ( m ) of the graph is given by:
$$ m = -2 $$
More Information
The slope reflects the steepness of the line. A slope of ( -2 ) indicates that for every 1 unit the line moves right, it moves 2 units down.
Tips
- Forgetting to use parentheses when calculating differences in the slope formula.
- Mixing up the coordinates; always remember that ((x_1, y_1)) should correspond to the first point and ((x_2, y_2)) to the second point.
