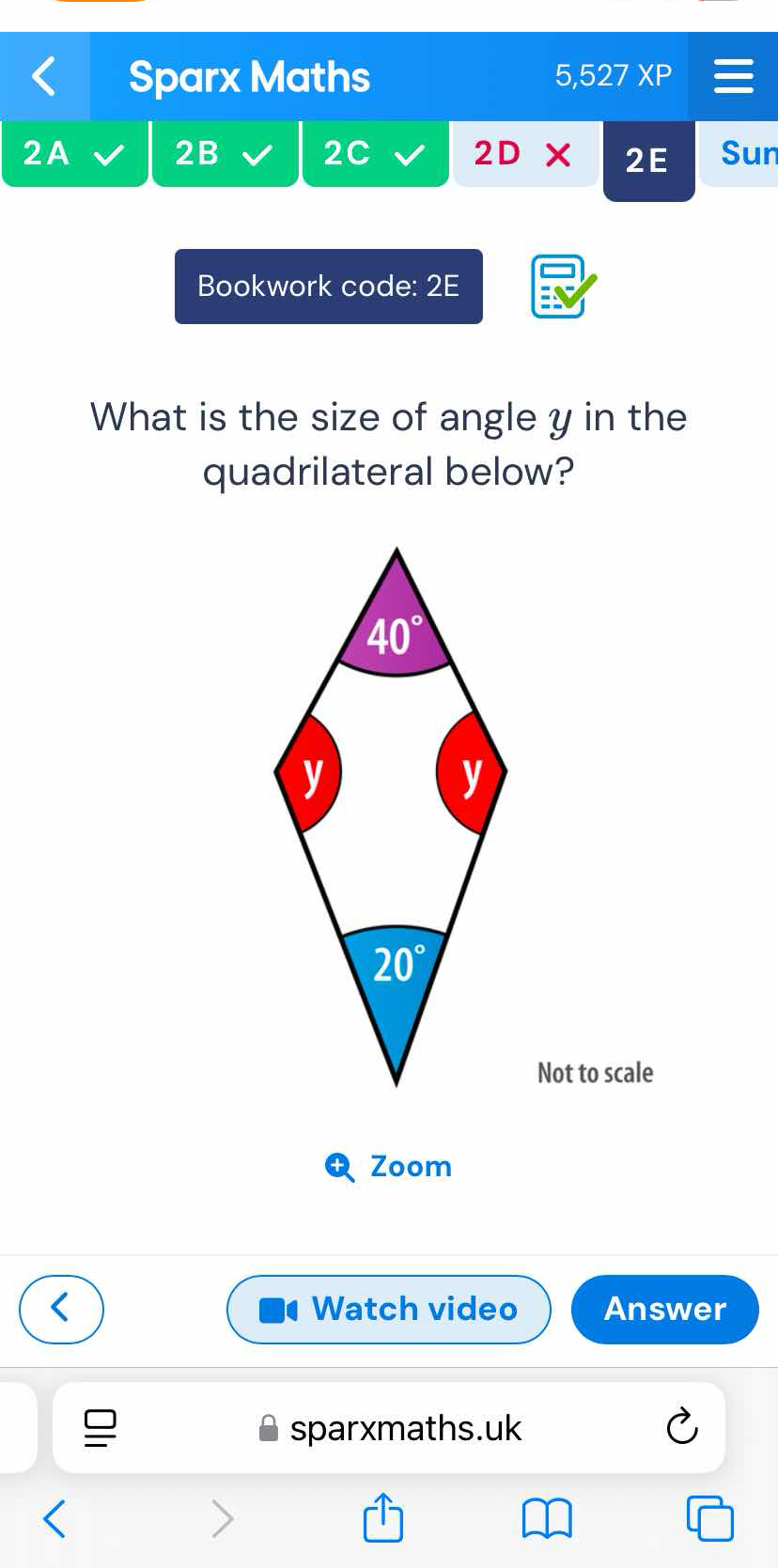
What is the size of angle y in the quadrilateral below?
Understand the Problem
The question is asking for the measurement of angle y in a given quadrilateral, where the other angles are labeled as 40° and 20°. To solve this, we would use the property that the sum of the interior angles in a quadrilateral is 360°.
Answer
The size of angle $y$ is $150°$.
Answer for screen readers
The size of angle $y$ is $150°$.
Steps to Solve
-
Identify the known angles The angles given in the quadrilateral are 40° and 20°.
-
Set up the equation for the sum of angles We know that the sum of the interior angles of a quadrilateral is 360°. This gives us the equation: $$ 40° + 20° + y + y = 360° $$
-
Simplify the equation Combine the known angles in the equation: $$ 60° + 2y = 360° $$
-
Isolate the variable Subtract 60° from both sides to solve for $y$: $$ 2y = 360° - 60° $$ This simplifies to: $$ 2y = 300° $$
-
Solve for y Divide both sides by 2 to find $y$: $$ y = \frac{300°}{2} = 150° $$
The size of angle $y$ is $150°$.
More Information
In a quadrilateral, the sum of the interior angles must always equal 360°, which is a fundamental property in geometry. This principle helps us solve for unknown angles by setting up equations based on known values.
Tips
- Forgetting the properties of angles: It's easy to forget that the angles must sum to 360°.
- Miscalculating the addition or division: Double-check your arithmetic to avoid simple errors.
AI-generated content may contain errors. Please verify critical information