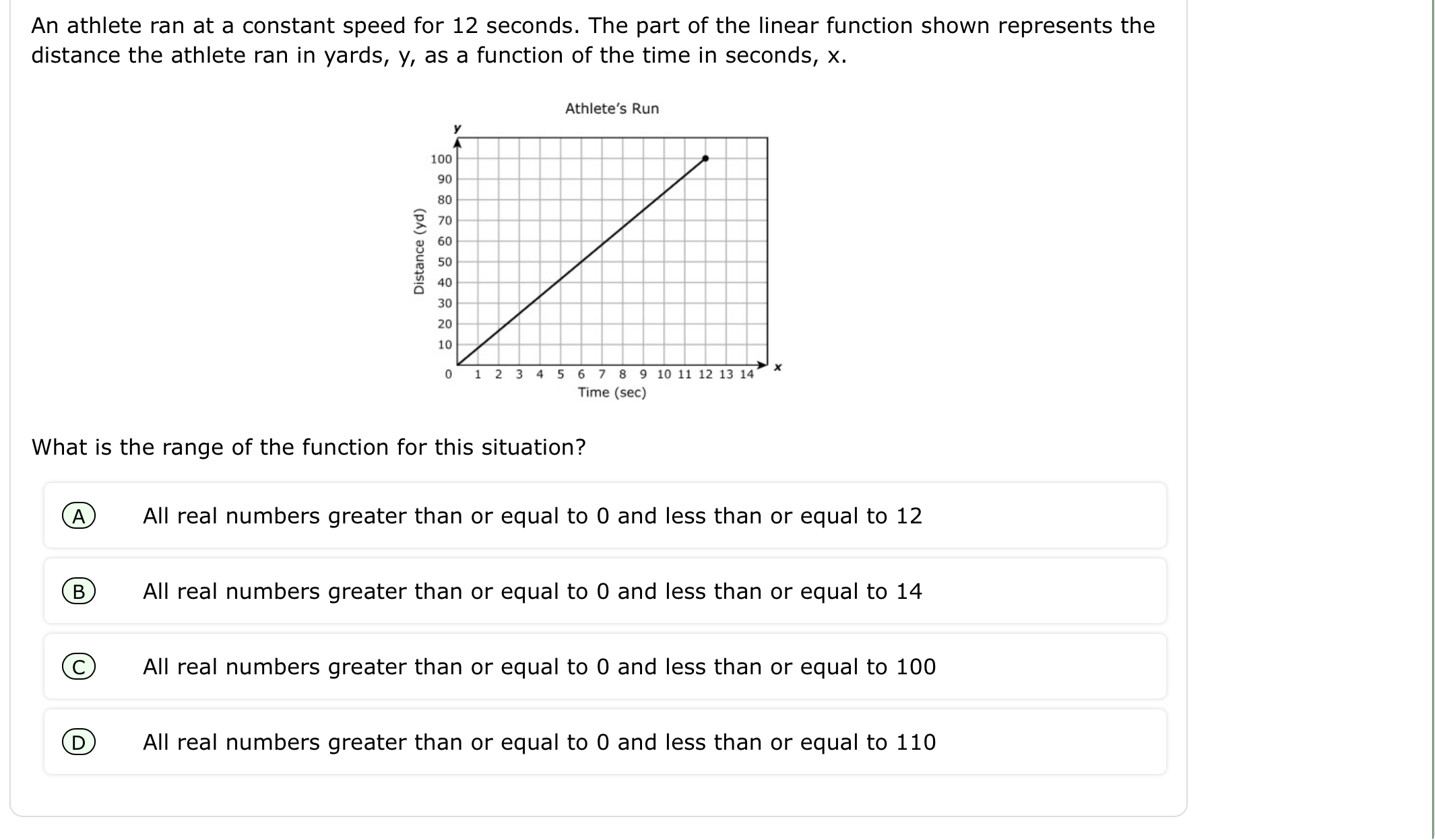
What is the range of the function for this situation?

Understand the Problem

The question is asking for the range of a linear function that represents the distance in yards run by an athlete over a time of 12 seconds. The answer should reflect the maximum distance that corresponds to that time on the given graph.

Answer

All real numbers greater than or equal to $0$ and less than or equal to $12$.

Steps to Solve

Identify the context of the problem

The problem presents a scenario where an athlete runs for 12 seconds. We need to find the range of the function that represents the distance (in yards) run over time (in seconds).

Determine the endpoints for time and distance

According to the graph, the time $x$ ranges from $0$ seconds to $12$ seconds. We look for the corresponding distance $y$ values at these endpoints.

Analyze the distance at the endpoint

From the graph, we observe that the maximum distance when $x = 12$ seconds is $y = 12$ yards. Thus, the distance varies from $0$ to $12$ yards.

Define the range of the function

The range reflects the possible output values of the function for $x$ between $0$ and $12$ seconds. The outputs correspond to the distances run, which are in the interval from $0$ to $12$ yards.

Summarize the findings

The range of the function is therefore all real numbers greater than or equal to $0$ and less than or equal to $12$.

The range of the function is: all real numbers greater than or equal to $0$ and less than or equal to $12$.

More Information

This means the athlete could run anywhere from $0$ yards (not moving) to $12$ yards during the 12 seconds. This analysis helps understand how distance relates to time in linear motion.

Tips

Misinterpreting the graph could lead to incorrect values for the distance.
Forgetting to consider both the lower and upper bounds of the range might affect the final answer.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!