ln(x^2 - 13x + 36) + 2ln(x - 4) - ln(x - 9)
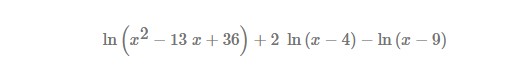
Understand the Problem
The question is asking for the simplification of a logarithmic expression involving natural logarithms and algebraic terms. We will use logarithmic properties to combine and simplify the expression step by step.
Answer
$\ln((x - 4)^3)$
Answer for screen readers
The simplified expression is $\ln((x - 4)^3)$.
Steps to Solve
- Apply the Property of Logarithms for Multiplication
Using the property of logarithms that states $a \ln(b) = \ln(b^a)$, we can simplify $2 \ln(x - 4)$:
$$ 2 \ln(x - 4) = \ln((x - 4)^2) $$
Now the expression becomes: $$ \ln(x^2 - 13x + 36) + \ln((x - 4)^2) - \ln(x - 9) $$
- Combine the Logarithmic Expressions
Next, we can apply the property of logarithms for addition which states that $\ln(a) + \ln(b) = \ln(ab)$:
$$ \ln(x^2 - 13x + 36) + \ln((x - 4)^2) = \ln((x^2 - 13x + 36)(x - 4)^2) $$
So now our expression is: $$ \ln((x^2 - 13x + 36)(x - 4)^2) - \ln(x - 9) $$
- Apply the Property of Logarithms for Subtraction
Using the property of logarithms for subtraction, which states that $\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right)$, we can write:
$$ \ln\left(\frac{(x^2 - 13x + 36)(x - 4)^2}{(x - 9)}\right) $$
- Factor the Quadratic Expression
Now, let's factor $x^2 - 13x + 36$: $$ x^2 - 13x + 36 = (x - 4)(x - 9) $$
Substituting this back into our expression, we get: $$ \ln\left(\frac{(x - 4)(x - 9)(x - 4)^2}{x - 9}\right) $$
- Simplify the Expression
The expression simplifies as follows: $$ \ln\left((x - 4)^3\right) $$
So the final simplified expression is: $$ \ln((x - 4)^3) $$
The simplified expression is $\ln((x - 4)^3)$.
More Information
This simplification demonstrates how logarithmic properties simplify expressions involving products and quotients. The factorization of the quadratic played a crucial role in arriving at the final answer.
Tips
- Misapplying logarithmic properties: Ensure that properties of logarithms are applied correctly, particularly the addition and subtraction rules.
- Failing to factor correctly: When factoring quadratic equations, it's essential to double-check the factors to avoid errors.
AI-generated content may contain errors. Please verify critical information