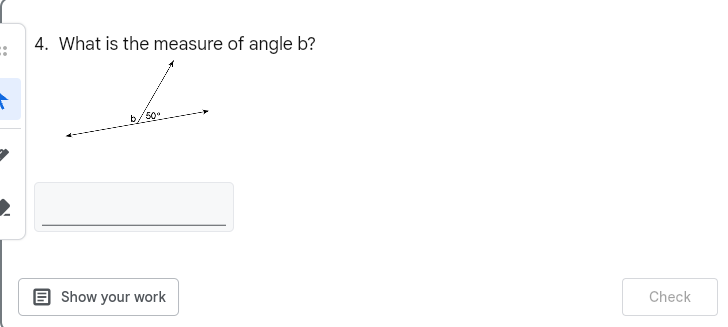
What is the measure of angle b?
Understand the Problem
The question is asking for the measure of angle b in a given geometric situation, likely involving angles and their relationships. To solve it, we would typically refer to properties of angles – such as supplementary, complementary, or vertical angles – depending on the diagram shown.
Answer
The measure of angle b is $130$ degrees.
Answer for screen readers
The measure of angle b is $130$ degrees.
Steps to Solve
-
Identify the given angles The diagram indicates that angle b and another angle (let's denote it as angle 50, which is labeled in the diagram) are likely related.
-
Recognize the relationship between angles If angle b and angle 50 are on a straight line, then they are supplementary. This means their measures add up to 180 degrees.
-
Set up the equation Since angle 50 is given as 50 degrees, we can express this relationship: $$ b + 50 = 180 $$
-
Solve for angle b Rearranging the equation to isolate angle b gives: $$ b = 180 - 50 $$
-
Calculate the value Now, we compute the value: $$ b = 130 $$
The measure of angle b is $130$ degrees.
More Information
Angle relationships are fundamental in geometry. Supplementary angles, which add up to 180 degrees, help solve many geometric problems easily.
Tips
- Confusing supplementary angles with complementary angles. Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees.
- Forgetting to subtract from 180 degrees in problems involving straight angles.
AI-generated content may contain errors. Please verify critical information