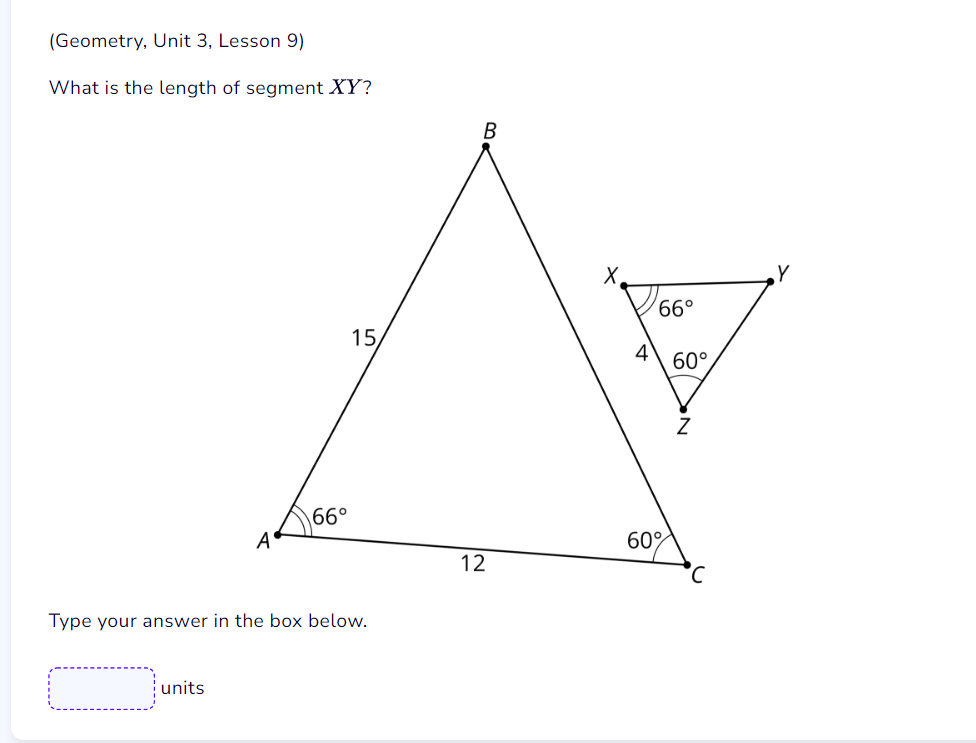
What is the length of segment XY?

Steps to Solve

1. Identify the triangles
   We have two triangles: triangle ABC and triangle XYZ. We know the lengths of sides in triangle ABC and parts of triangle XYZ.

2. Use the Law of Sines on triangle ABC
   To find side ( AC ), we can apply the Law of Sines:
   $$ \frac{AB}{\sin(C)} = \frac{AC}{\sin(B)} $$
   Where ( AB = 15 ), ( AC = 12 ), ( \angle B = 60^\circ ), and ( \angle C = 66^\circ ).

3. Calculate side AC
   Substituting the known values into the formula:
   $$ \frac{15}{\sin(60^\circ)} = \frac{12}{\sin(66^\circ)} $$
   Cross multiplying to solve for ( AC ):
   $$ AC = \frac{12 \cdot \sin(60^\circ)}{\sin(66^\circ)} $$

4. Compute lengths using Law of Sines on triangle XYZ
   Using the Law of Sines again for triangle XYZ to find segment ( XY ):
   $$ \frac{XZ}{\sin(Y)} = \frac{XY}{\sin(Z)} $$
   Where ( XZ = 4 ), ( \angle Y = 66^\circ ), and ( \angle Z = 60^\circ ).

5. Calculate length XY
   Substituting the known values:
   $$ \frac{4}{\sin(60^\circ)} = \frac{XY}{\sin(66^\circ)} $$
   Now solve for ( XY ):
   $$ XY = \frac{4 \cdot \sin(66^\circ)}{\sin(60^\circ)} $$

6. Final computation
   Now compute the values of ( XY ) for the final answer.