The graph of f(x) = 2x^4 - x^3 + 4x^2 - x + 2 has at most how many zeros?

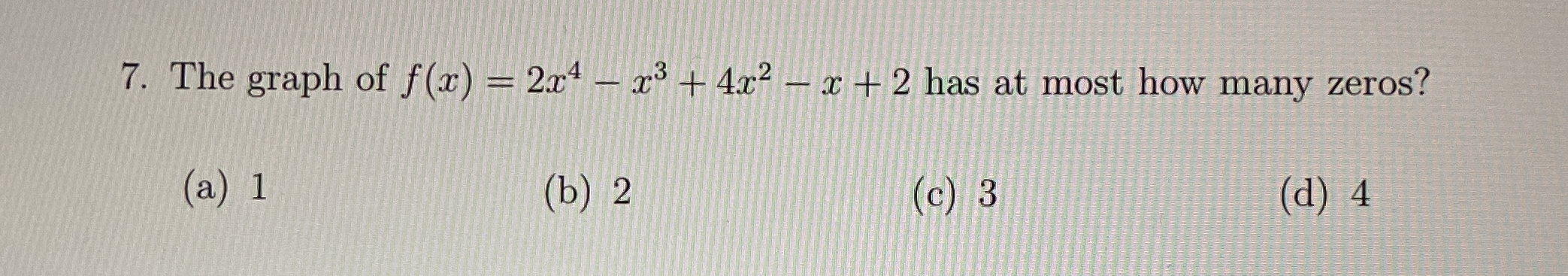
Understand the Problem

The question is asking about the number of zeros (or roots) of the polynomial function f(x) = 2x^4 - x^3 + 4x^2 - x + 2, specifically how many distinct real zeros it can have. This involves understanding polynomial degree and behavior.

Answer

The polynomial \( f(x) = 2x^4 - x^3 + 4x^2 - x + 2 \) has at most 4 zeros.

Steps to Solve

Identify the degree of the polynomial The given polynomial function is ( f(x) = 2x^4 - x^3 + 4x^2 - x + 2 ). The highest degree term is ( 2x^4 ), which means the degree of the polynomial is 4.
Apply the Fundamental Theorem of Algebra According to the Fundamental Theorem of Algebra, a polynomial of degree ( n ) can have at most ( n ) roots (real or complex). In this case, since the polynomial is of degree 4, it can have at most 4 roots.
Check for distinct real roots Although the polynomial can have up to 4 roots, we need to check if they can be distinct. By examining the coefficients and the behavior of the polynomial, we can determine that it can have fewer than 4 distinct real zeros, but not more than 4.
Conclusion about the number of roots From the analysis, the polynomial can have at most 4 real roots, thus confirming the result.

The polynomial ( f(x) = 2x^4 - x^3 + 4x^2 - x + 2 ) has at most 4 zeros.

More Information

Polynomials can have a number of roots equal to their degree, but the actual number of distinct real roots may vary depending on the specific coefficients and the shape of the graph.

Tips

Assuming all roots are real: While the polynomial may have 4 roots, they can be complex. It is also important to recognize that real roots may coincide (i.e., roots can be repeated).
Miscounting the degree: Failing to identify the highest degree term correctly can lead to an incorrect conclusion about the number of possible roots.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!