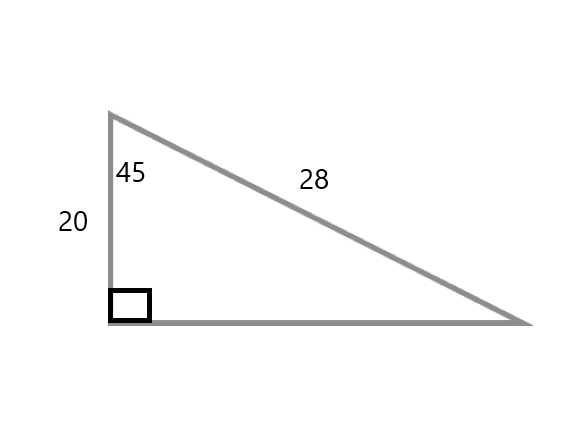
What is the hypotenuse of the triangle with sides 20 and 28?
Understand the Problem
The question is likely related to calculating dimensions or properties of the triangle in the image, such as finding the length of the hypotenuse or using the provided side lengths. This problem can be addressed using the Pythagorean theorem or trigonometry.
Answer
The triangle is not a right triangle.
Answer for screen readers
The triangle is not a right triangle.
Steps to Solve
- Identify triangle dimensions
The triangle given has a vertical side of length (20), a horizontal side of length (28), and a hypotenuse of length (45). We can verify if this is a right triangle using the Pythagorean theorem.
- Apply the Pythagorean theorem
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. We express this as:
$$ c^2 = a^2 + b^2 $$
In our case, let ( c = 45 ), ( a = 20 ), and ( b = 28 ).
- Calculate (a^2 + b^2)
Now, we calculate:
$$ a^2 + b^2 = 20^2 + 28^2 $$
Calculating each square:
$$ 20^2 = 400 $$
$$ 28^2 = 784 $$
Adding them:
$$ a^2 + b^2 = 400 + 784 = 1184 $$
- Calculate (c^2)
Next, calculate ( c^2 ):
$$ c^2 = 45^2 $$
Calculating:
$$ 45^2 = 2025 $$
- Compare the results
Now, we compare ( c^2 ) and ( a^2 + b^2 ):
Since ( 2025 ) (which is ( c^2 )) is not equal to ( 1184 ) (which is ( a^2 + b^2 )), the triangle is not a right triangle.
The triangle is not a right triangle.
More Information
This triangle's sides do not satisfy the Pythagorean theorem, indicating that it does not form a right angle. This is important in geometry for understanding relationships between triangle sides.
Tips
- Mistaking the side lengths as valid for a right triangle without verifying with the Pythagorean theorem.
- Miscalculating the squares of the side lengths.