What is the glucose in the sample in milligram per 100 ml?

Steps to Solve

1. Identify the Given Data

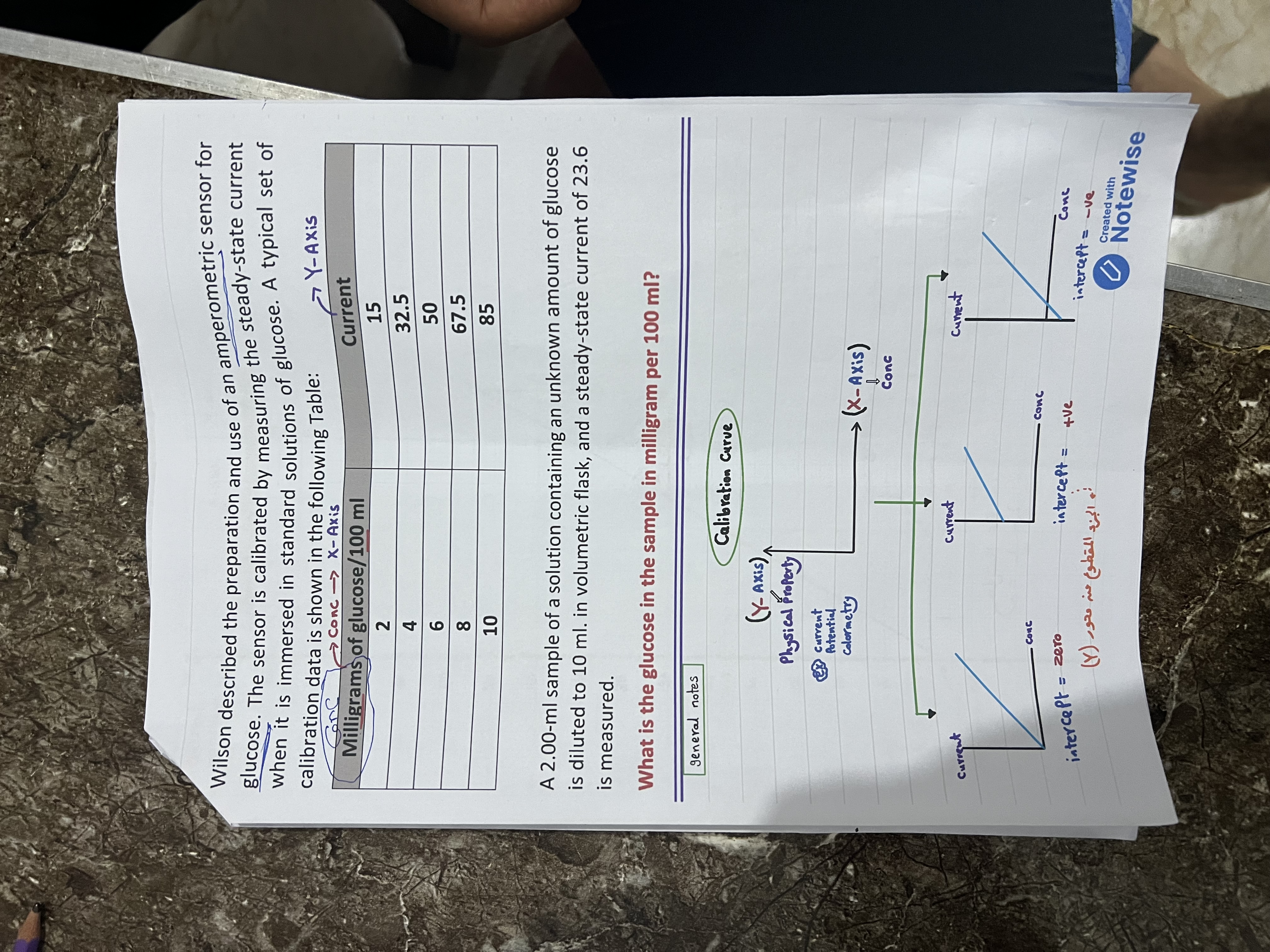
We have the steady-state current measurement of the sample, which is 23.6. We also have a calibration curve data as follows:

[ \begin{array}{|c|c|} \hline \text{Milligrams of glucose/100 ml} & \text{Current} \ \hline 2 & 15 \ 4 & 32.5 \ 6 & 50 \ 8 & 67.5 \ 10 & 85 \ \hline \end{array} ]

2. Determine the Linear Relationship

To find the relationship between current and glucose concentration, we can use linear regression or observation on the data points. The equation of the line will be in the form:

$$ y = mx + b $$

where ( y ) is the current, ( x ) is the concentration (in mg/100ml), ( m ) is the slope, and ( b ) is the y-intercept.

3. Calculate the Slope (m)

Using two data points, for instance, (2, 15) and (10, 85):

[ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{85 - 15}{10 - 2} = \frac{70}{8} = 8.75 ]

4. Determine the y-Intercept (b)

Using one of the points, for example, (2, 15):

[ y = mx + b \implies 15 = 8.75(2) + b \implies b = 15 - 17.5 = -2.5 ]

5. Formulate the Equation

Now substituting ( m ) and ( b ) into the linear equation:

[ \text{Current} = 8.75 \times \text{Concentration} - 2.5 ]

6. Substitute the Current Value

Now we substitute the measured current (23.6) into the equation to solve for concentration:

[ 23.6 = 8.75 \times \text{Concentration} - 2.5 ]

7. Solve for Concentration

Rearranging the equation:

[ 8.75 \times \text{Concentration} = 23.6 + 2.5 = 26.1 ]

Divide both sides by 8.75 to find the concentration:

[ \text{Concentration} = \frac{26.1}{8.75} \approx 2.97 \text{ mg/100 ml} ]

8. Adjust for the Dilution Factor

Since the sample was diluted from 2.00 ml to 10 ml, we need to account for this dilution. The dilution factor is:

$$ \text{Dilution Factor} = \frac{10 \text{ ml}}{2 \text{ ml}} = 5 $$

Hence, the concentration in the original solution is:

[ \text{Final Concentration} = 2.97 \times 5 = 14.85 \text{ mg/100 ml} ]