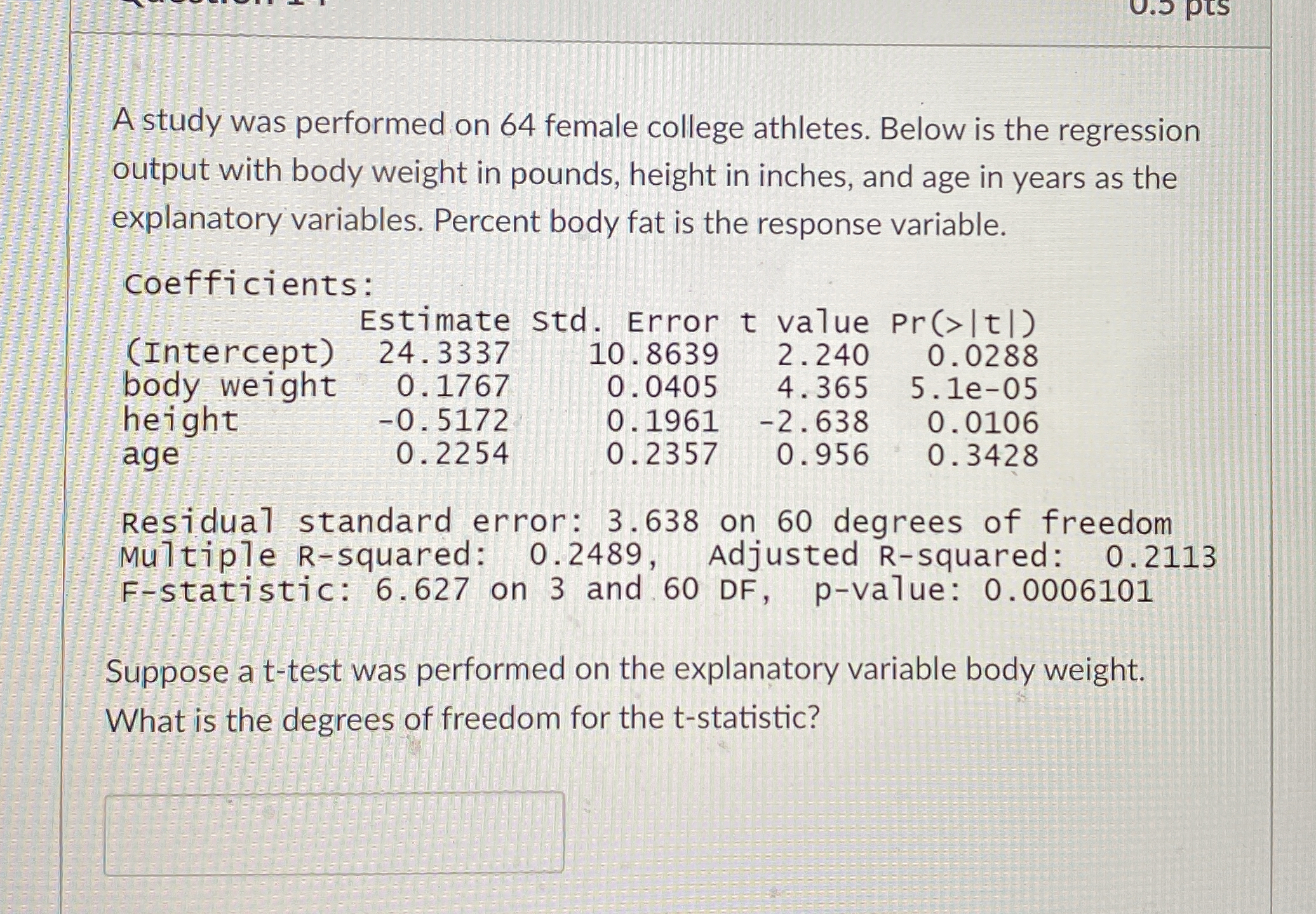
What is the degrees of freedom for the t-statistic?

Understand the Problem

The question asks for the degrees of freedom associated with the t-statistic from a t-test performed on the explanatory variable body weight, using the regression analysis output provided.

Answer

$60$

Steps to Solve

Identify the number of observations

The total number of observations (sample size) is given as 64 female college athletes.

Identify the number of predictors

In the regression output, the explanatory variables listed are body weight, height, and age. This means that there are 3 predictors in the model.

Calculate the degrees of freedom for the t-statistic

The degrees of freedom (DF) for the t-statistic in a t-test can be calculated using the formula: $$ \text{DF} = n - p - 1 $$ where:

$n$ is the total number of observations,
$p$ is the number of predictors.

Here:

$n = 64$ (total observations)
$p = 3$ (body weight, height, age)

Therefore, the calculation is: $$ \text{DF} = 64 - 3 - 1 = 60 $$

The degrees of freedom for the t-statistic is $60$.

More Information

In regression analysis, the degrees of freedom for a t-test involving an individual predictor are important for determining the statistical significance of that predictor. Here, the value is consistent with the residual standard error that was also reported as having 60 degrees of freedom.

Tips

Confusing the total sample size with the degrees of freedom. Make sure to subtract the number of predictors and 1 from the sample size.
Not accounting for all predictors in the model when calculating degrees of freedom.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!