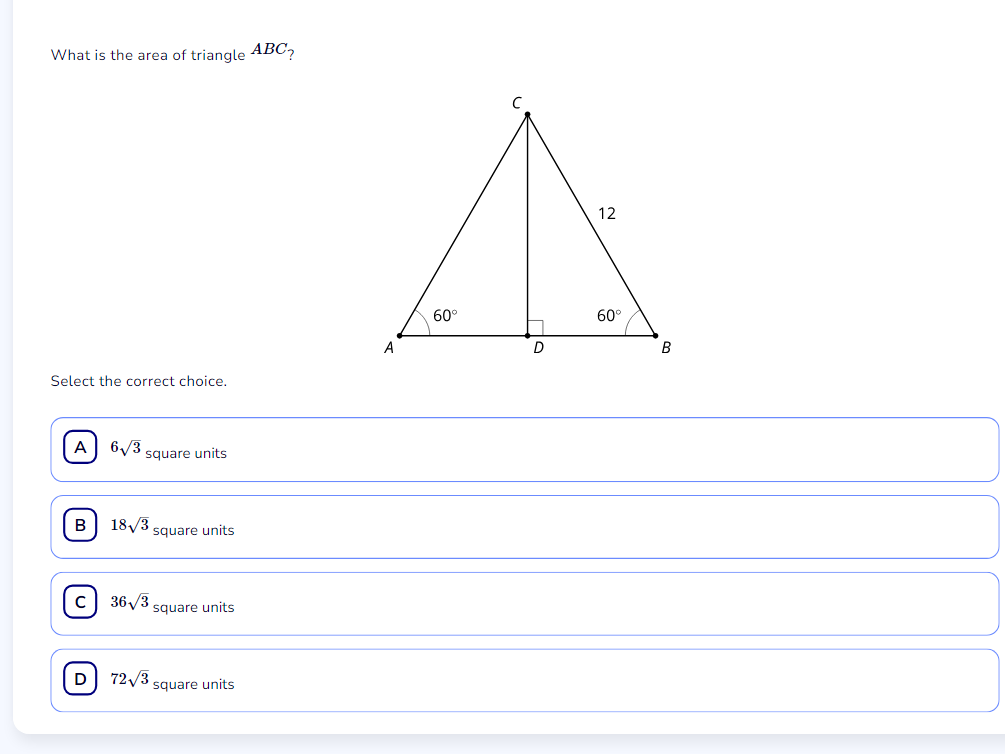
What is the area of triangle ABC?

Steps to Solve

1. Identify the areas' basic formula

To find the area of triangle $ABC$, we use the formula for the area:

$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $$

2. Determine the height and base

The height from point $C$ to line $AB$ is given as 12 units.

To find the base $AB$, we need to calculate the length of $AD$ (where $D$ is the foot of the height from $C$ to line $AB$).

3. Calculate length using trigonometric functions

Since $\angle CAD = 60°$, we can use:

$$ \tan(60°) = \frac{CD}{AD} $$

We know $CD = 12$. Therefore, we can set up the equation:

$$ \sqrt{3} = \frac{12}{AD} $$

Solving for $AD$ gives:

$$ AD = \frac{12}{\sqrt{3}} = 4\sqrt{3} $$

4. Find the length of base $AB$

Since triangle $ADC$ is a right triangle, and $AD + DB = AB$, we need to find the length of $DB$. Because $\angle ABC = 60°$ as well, $DB$ will also equal $AD$ due to the symmetry of the triangle. Therefore,

$$ DB = AD = 4\sqrt{3} $$

So, the total length of base $AB$ will be:

$$ AB = AD + DB = 4\sqrt{3} + 4\sqrt{3} = 8\sqrt{3} $$

5. Calculate the area of triangle $ABC$

Substitute the base and height into the area formula:

$$ \text{Area} = \frac{1}{2} \times (8\sqrt{3}) \times 12 $$

Calculating this yields:

$$ \text{Area} = \frac{1}{2} \times 96\sqrt{3} = 48\sqrt{3} $$