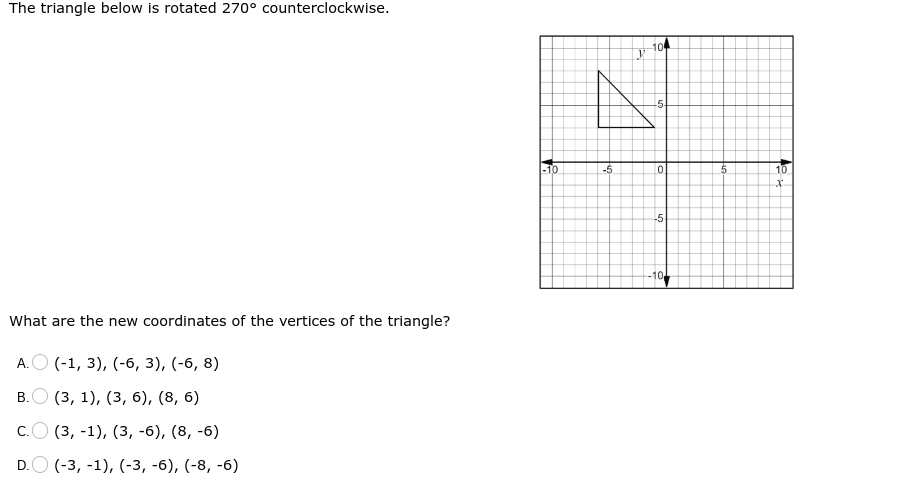
What are the new coordinates of the vertices of the triangle after it is rotated 270° counterclockwise?
Understand the Problem
The question is asking for the new coordinates of the vertices of a triangle after it has been rotated 270° counterclockwise. To solve this, we will apply the rotation transformation to each vertex of the triangle and find the new positions based on the rotation rules.
Answer
The new coordinates of the vertices are $ (3, 1), (3, 6), (-8, 6) $.
Answer for screen readers
The new coordinates of the vertices of the triangle are: $ (3, 1), (3, 6), (-8, 6) $
Steps to Solve
-
Understand the rotation transformation To rotate a point $(x, y)$ counterclockwise by $270^\circ$, use the transformation rule: $$ (x', y') = (y, -x) $$
-
Apply the transformation to each vertex Identify the original vertices of the triangle. For each vertex $(x, y)$, apply the rotation transformation.
-
Vertex 1: For the point $(-1, 3)$:
- New coordinates: $(3, 1)$
-
Vertex 2: For the point $(-6, 3)$:
- New coordinates: $(3, 6)$
-
Vertex 3: For the point $(-6, -8)$:
- New coordinates: $(-8, 6)$
- List the new coordinates After applying the transformation, the new coordinates of the vertices are:
- Vertex 1: $(3, 1)$
- Vertex 2: $(3, 6)$
- Vertex 3: $(-8, 6)$
The new coordinates of the vertices of the triangle are: $ (3, 1), (3, 6), (-8, 6) $
More Information
When performing a $270^\circ$ counterclockwise rotation, the new coordinates reflect the nature of the transformation which changes both x and y values by switching their places and inverting the new x-coordinate.
Tips
- Misapplying the transformation formula by reversing the signs or the order of $x$ and $y$.
- Confusing between $270^\circ$ and $90^\circ$ rotations. Ensure upon rotation you correctly understand the degree applied.
AI-generated content may contain errors. Please verify critical information