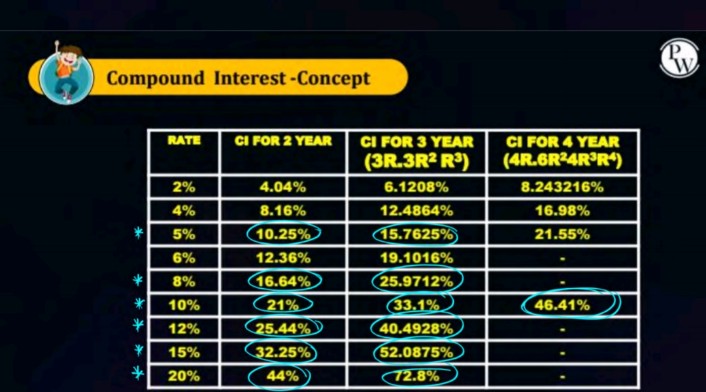
What does the table of compound interest represent for different rates and time periods?

Steps to Solve

1. Understanding Compound Interest Compound interest refers to the interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods.

2. Identify the Rate From the table, you can see various interest rates (2%, 4%, 5%, up to 20%) and their respective compound interests for 2, 3, and 4 years.

3. Select a Rate and Year Choose a specific interest rate and period from the table. For example, if we select a rate of 10% for 3 years, we can find that the compound interest is 33.1%.

4. Use the Formula for Compound Interest The formula for calculating compound interest is: $$ A = P(1 + \frac{r}{n})^{nt} $$ Where:

• ( A ) is the amount of money accumulated after n years, including interest.
• ( P ) is the principal amount (the initial sum of money).
• ( r ) is the annual interest rate (decimal).
• ( n ) is the number of times that interest is compounded per year.
• ( t ) is the time the money is invested or borrowed in years.

5. Calculate Compound Interest If calculating the compound interest yourself:
   For example, for a principal ( P = 1000 ), rate ( r = 0.10 ), compounded annually ( (n = 1) ), and time ( t = 3 ): $$ A = 1000(1 + \frac{0.10}{1})^{1 \times 3} = 1000(1.10)^3 \approx 1331 $$ The compound interest would be: $$ CI = A - P = 1331 - 1000 = 331 $$