3 x 10^3 + 2 x 10^1 + 4 x 10^x + 5 x 10^y = 30.24. Write down the value of x and y.

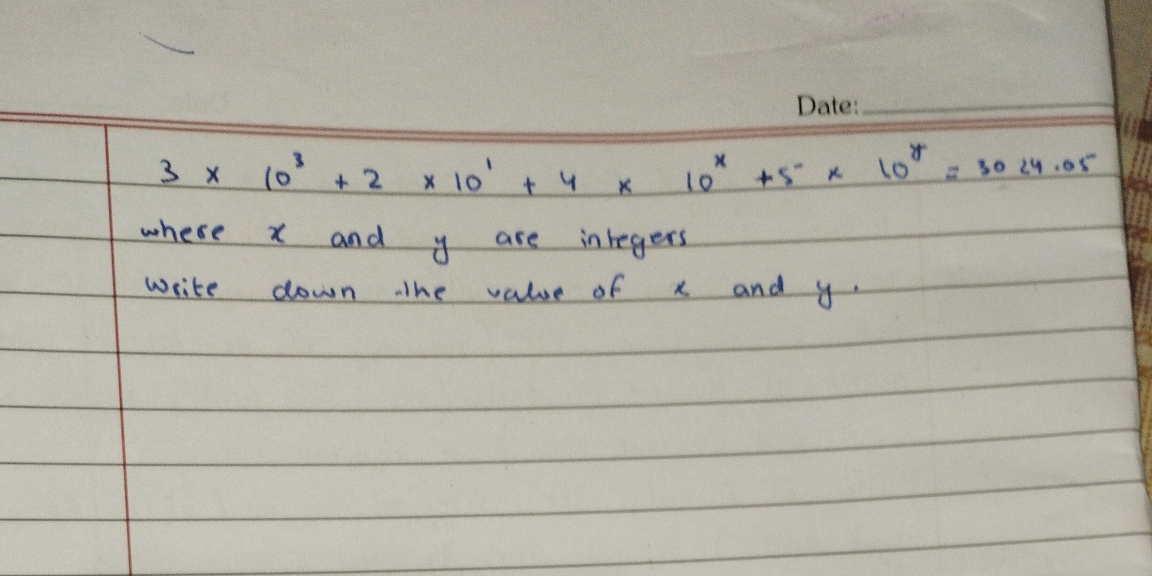
Understand the Problem

The question is asking for the values of the integers x and y in a mathematical expression involving powers of ten that equals 30.24. The user needs to simplify or rearrange the equation to find the values of x and y.

Answer

No integer values for $ x $ and $ y $ satisfy the equation.

Steps to Solve

Convert the equation to simpler terms

Rewrite the equation using the values calculated from powers of ten.

[ 3 \times 10^3 = 3000, \quad 2 \times 10^1 = 20 ]

So the equation becomes:

[ 3000 + 20 + 4 \times 10^x + 5 \times 10^y = 30.24 ]

Combine constant terms

Add the constant terms together:

[ 3000 + 20 = 3020 ]

The equation now simplifies to:

[ 3020 + 4 \times 10^x + 5 \times 10^y = 30.24 ]

Isolate the variable terms

Rearrange the equation to isolate the terms involving $x$ and $y$:

[ 4 \times 10^x + 5 \times 10^y = 30.24 - 3020 ]

Calculating the right side gives:

[ 4 \times 10^x + 5 \times 10^y = -2989.76 ]

Analyze possible values of ( x ) and ( y )

Since $10^x$ and $10^y$ are powers of 10 and cannot yield negative results, there are no integer values for ( x ) and ( y ) that satisfy this condition.

There are no integer values for ( x ) and ( y ) such that ( 3 \times 10^3 + 2 \times 10^1 + 4 \times 10^x + 5 \times 10^y = 30.24 ).

More Information

This problem demonstrates that when trying to express a sum of positive powers of ten equaling a negative number, it is impossible for integer values. Thus, in problems involving powers of ten, ensuring the resultant value remains positive is crucial.

Tips

Miscalculating the sum of the constant terms, which can lead to incorrect simplifications.
Not recognizing that powers of ten cannot yield negative results.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!