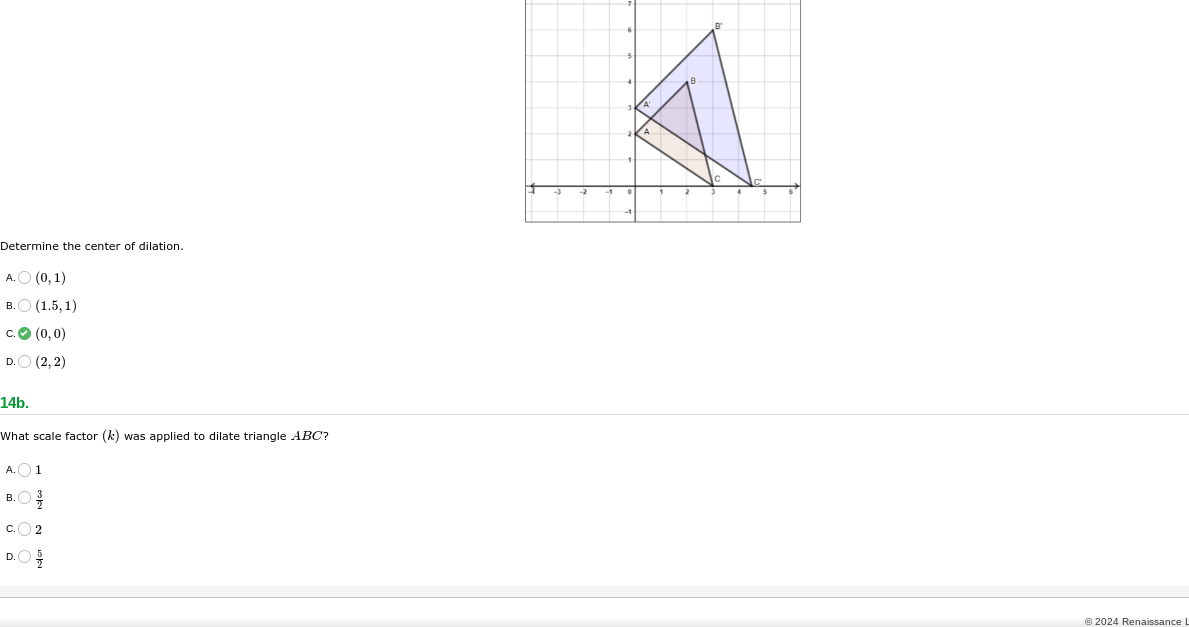
Determine the center of dilation for triangle ABC and what scale factor was applied to dilate triangle ABC.
Understand the Problem
The question is asking to determine the center of dilation for a triangle and to find the scale factor applied to dilate triangle ABC. This involves understanding geometric transformations, specifically dilation, and requires analyzing the coordinates of the triangle.
Answer
Center of dilation is $(0, 0)$, and the scale factor is $k = \frac{3}{2}$.
Answer for screen readers
Center of dilation: $(0, 0) \quad k = \frac{3}{2}$.
Steps to Solve
- Identify the Center of Dilation
To determine the center of dilation, observe the original triangle ABC and its dilated version A'B'C'. The center of dilation is the point from which all points of the triangle are proportionally extended or reduced.
- Check the Coordinates of Triangle Vertices
Find the coordinates of the original triangle ABC and the dilated triangle A'B'C'. For instance, if the coordinates of A, B, C are (x₁, y₁), (x₂, y₂), (x₃, y₃), and respective coordinates of A', B', and C' are (x₁', y₁'), (x₂', y₂'), (x₃', y₃').
- Use Ratio Concept
The relationship between the original coordinates and the dilated coordinates can be expressed as follows:
$$ x' = k(x - c_x) + c_x \quad \text{and} \quad y' = k(y - c_y) + c_y $$
where $(c_x, c_y)$ is the center of dilation and $k$ is the scale factor.
- Choosing the Center
From the options given, plug in coordinate values to see which one produces proportional relationships observed between original and dilated coordinates.
- Calculating the Scale Factor
The scale factor $k$ can be found by comparing corresponding coordinates:
$$ k = \frac{A'}{A} \quad \text{for a point A} $$
You would use any point from the original triangle and its corresponding point in the dilated triangle to find $k$.
- Select the Scale Factor
From the calculated $k$, determine which answer choice matches.
Center of dilation: $(0, 0) \quad k = \frac{3}{2}$.
More Information
The center of dilation determines how the points of the triangle scale in relation to each other. The scale factor indicates how much larger or smaller the triangle has become compared to its original size.
Tips
- Incorrect center of dilation: Confusing how the coordinates relate in dilation can lead to selecting the wrong center.
- Miscalculating scale factor: Not keeping consistent when calculating the relationship between original and transformed coordinates can lead to errors in finding $k$.
AI-generated content may contain errors. Please verify critical information