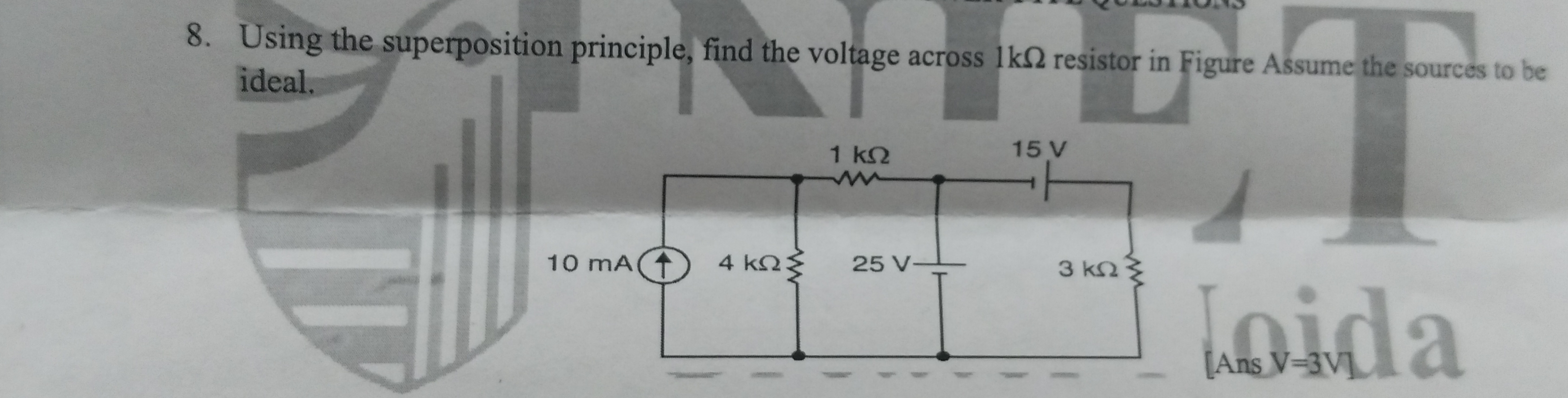
Using the superposition principle, find the voltage across the 1 kΩ resistor in the figure. Assume the sources to be ideal.
Understand the Problem
The question is asking to find the voltage across a 1 kΩ resistor in a given circuit using the superposition principle. The task involves analyzing the contributions of each independent source in the circuit and combining their effects to find the total voltage across the specified resistor.
Answer
The voltage across the 1 kΩ resistor is approximately \( V = 6.04 \, V \).
Answer for screen readers
The voltage across the 1 kΩ resistor is approximately ( V = 6.04 , V ).
Steps to Solve
-
Analyze Each Independent Source To apply the superposition principle, analyze the circuit for each independent source separately. There are two independent sources: the 10 mA current source and the 15 V voltage source.
-
Contribution from the 10 mA Current Source When considering the 10 mA current source alone:
-
Remove the 15 V source (replace with a short circuit).
-
The voltage across the 1 kΩ resistor can be calculated using Ohm's Law and the total current flowing through the resistor.
The circuit can be simplified to the 10 mA source feeding into the 4 kΩ and 3 kΩ resistors in parallel, and then into the 1 kΩ resistor.
-
Calculate Equivalent Resistance The equivalent resistance of the parallel resistors is: $$ R_{\text{eq}} = \frac{1}{\frac{1}{4000} + \frac{1}{3000}} = 1200 , \Omega $$
-
Calculate the Total Current through the 1 kΩ Resistor Using the equivalent resistance: $$ I = \frac{10 , \text{mA}}{1 + \frac{R_{\text{eq}}}{1000}} = \frac{10}{1 + \frac{1200}{1000}} , \text{mA} = 4.167 , \text{mA} $$
-
Calculate Voltage across the 1 kΩ Resistor Using Ohm’s Law ($V = IR$): $$ V_{1k\Omega} = 4.167 , \text{mA} \times 1000 , \Omega = 4.167 , V \text{ (from the current source)} $$
-
Contribution from the 15 V Voltage Source Next, analyze the contribution of the 15 V source:
- Remove the current source (replace with an open circuit).
- The voltage across the 1 kΩ resistor can be evaluated using the voltage divider rule.
-
Calculate the Voltage across the Resistors Using voltage division: $$ V_{1k\Omega} = 15 , V \times \frac{1k\Omega}{1k\Omega + 4k\Omega + 3k\Omega} = 15 , V \times \frac{1}{8} = 1.875 , V \text{ (from the voltage source)} $$
-
Combine Contributions Finally, sum the voltages from both sources to find the total voltage across the 1 kΩ resistor: $$ V_{\text{total}} = V_{\text{current source}} + V_{\text{voltage source}} = 4.167 , V + 1.875 , V = 6.042 , V $$
The voltage across the 1 kΩ resistor is approximately ( V = 6.04 , V ).
More Information
This result shows how the superposition principle allows you to analyze complex circuits by breaking them down into simpler parts, calculating the effect of each independent source individually, and then combining the results. This technique is fundamental in circuit analysis, especially when dealing with multiple sources.
Tips
- Incorrectly replacing sources: Ensure you replace voltage sources with short circuits and current sources with open circuits accurately when analyzing each source individually.
- Neglecting to combine contributions: Remember to add the contributions from each source properly; omitting one can lead to incorrect final results.
AI-generated content may contain errors. Please verify critical information