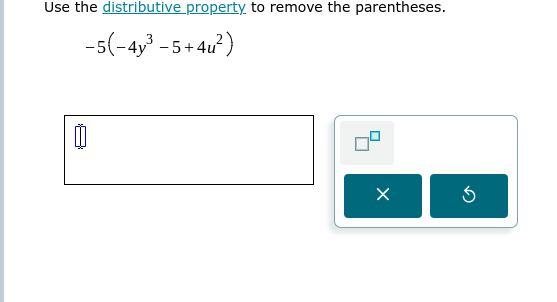
Use the distributive property to remove the parentheses: -5(-4y^3 - 5 + 4u^2)
Understand the Problem
The question is asking to apply the distributive property to simplify the given expression by removing the parentheses. This will involve multiplying -5 by each term inside the parentheses.
Answer
$$ 20y^3 + 25 - 20u^2 $$
Answer for screen readers
The simplified expression is: $$ 20y^3 + 25 - 20u^2 $$
Steps to Solve
-
Identify the expression We start with the expression: $$ -5(-4y^3 - 5 + 4u^2) $$
-
Apply the distributive property Multiply -5 by each term inside the parentheses, distributing it as follows: $$ -5 \cdot (-4y^3) $$ $$ -5 \cdot (-5) $$ $$ -5 \cdot (4u^2) $$
-
Perform each multiplication Calculate the products:
- For the first term: $$ -5 \cdot (-4y^3) = 20y^3 $$
- For the second term: $$ -5 \cdot (-5) = 25 $$
- For the third term: $$ -5 \cdot (4u^2) = -20u^2 $$
-
Combine the results Combine all the products: $$ 20y^3 + 25 - 20u^2 $$
The simplified expression is: $$ 20y^3 + 25 - 20u^2 $$
More Information
This result uses the distributive property, which states that $a(b + c) = ab + ac$. It's an essential concept in algebra for simplifying expressions.
Tips
- Forgetting to distribute the negative sign correctly can lead to incorrect signs in the final expression. Always pay attention to the signs when multiplying.
AI-generated content may contain errors. Please verify critical information