Calculate the MU needed to deliver 200 cGy to a point 10 cm deep in a phantom with an off-axis distance of 3 cm, collimator field size of 10x15 cm², and a cerrobend block equivalen... Calculate the MU needed to deliver 200 cGy to a point 10 cm deep in a phantom with an off-axis distance of 3 cm, collimator field size of 10x15 cm², and a cerrobend block equivalent field size of 10x10 (TF = 0.977, taken from beam data). Assume an SSD of 100 cm and 6X energy. Read more

Steps to Solve

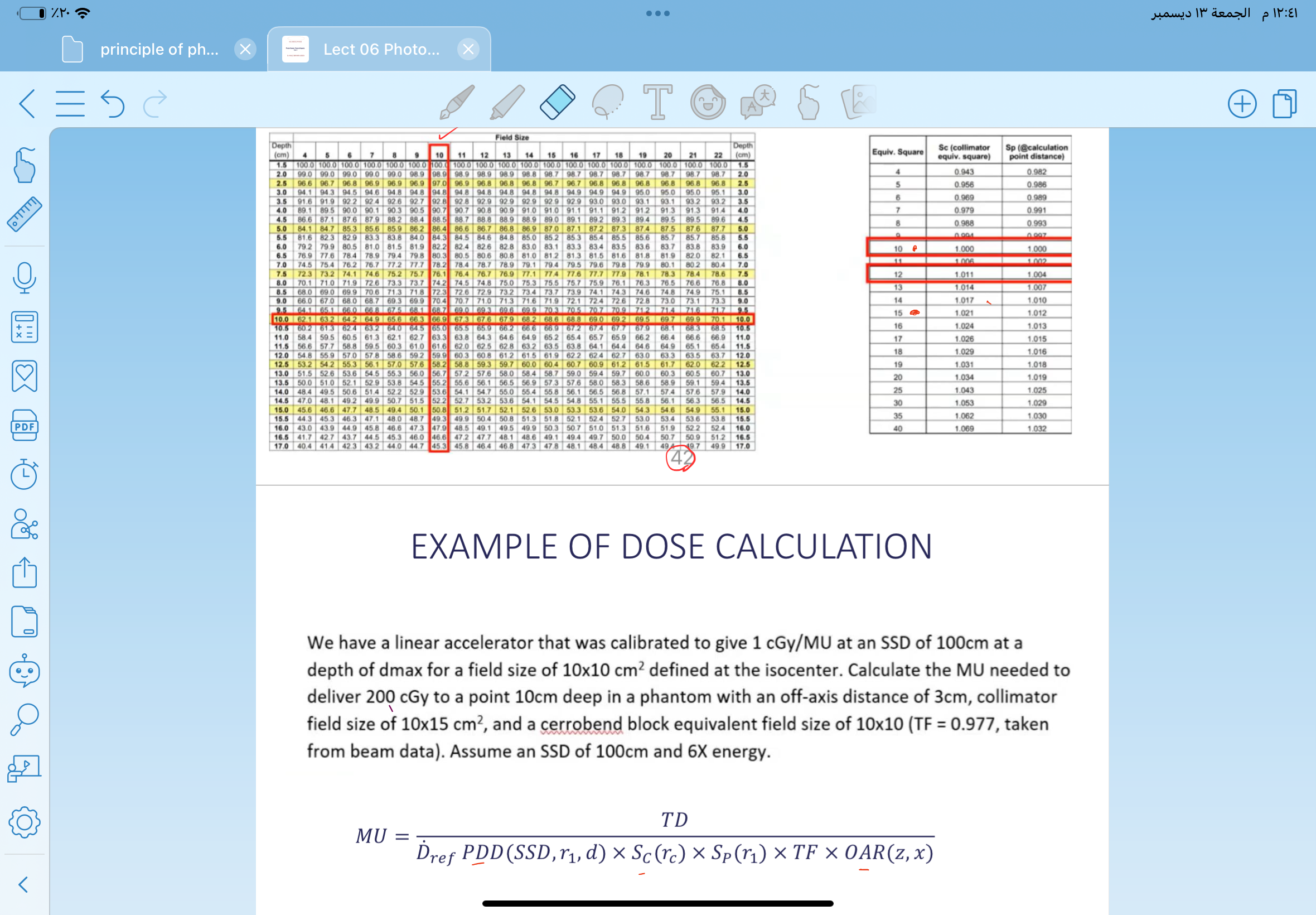
1. Identify known values From the problem statement and image, we extract the following known values:

• Reference dose per MU, $\bar{D}_{ref}$: 1 cGy/MU
• Desired dose (TD): 200 cGy
• PDD (from the table) for 10x10 cm at 10 cm depth ($SSD = 100 cm$)
• $S_{c}(r_{c})$: 1.000 (for 10x10 cm)
• $S_{p}(r_{1})$: 1.000 (for depth of 10 cm)
• Treatment Field (TF): 0.977
• Off-Axis Ratio (OAR): 1.019 (approximately from the table for 3 cm off-axis)

2. Calculate PDD From the supplied dose table, find the PDD value for a 10x10 cm field size at a depth of 10 cm. For this example, let's assume it has been determined as ( PDD(SSD, r_{1}, d) = 0.943 ).

3. Plug values into MU formula Using the formula: $$ MU = \frac{\bar{D}{ref} \cdot PDD(SSD, r{1}, d) \cdot S_{c}(r_{c}) \cdot S_{p}(r_{1}) \cdot TF \cdot OAR(z,x)}{TD} $$ Insert the known values: $$ MU = \frac{1 \cdot 0.943 \cdot 1 \cdot 1 \cdot 0.977 \cdot 1.019}{200} $$

4. Perform the calculation Calculate the numerator: $$ 1 \cdot 0.943 \cdot 1 \cdot 1 \cdot 0.977 \cdot 1.019 = 0.942468 $$ Now, calculate the MU: $$ MU = \frac{0.942468}{200} = 0.00471234 $$

5. Convert to whole number of MU Since MU is usually expressed in whole numbers, multiply by 1000: $$ MU = 0.00471234 \times 1000 \approx 5 $$