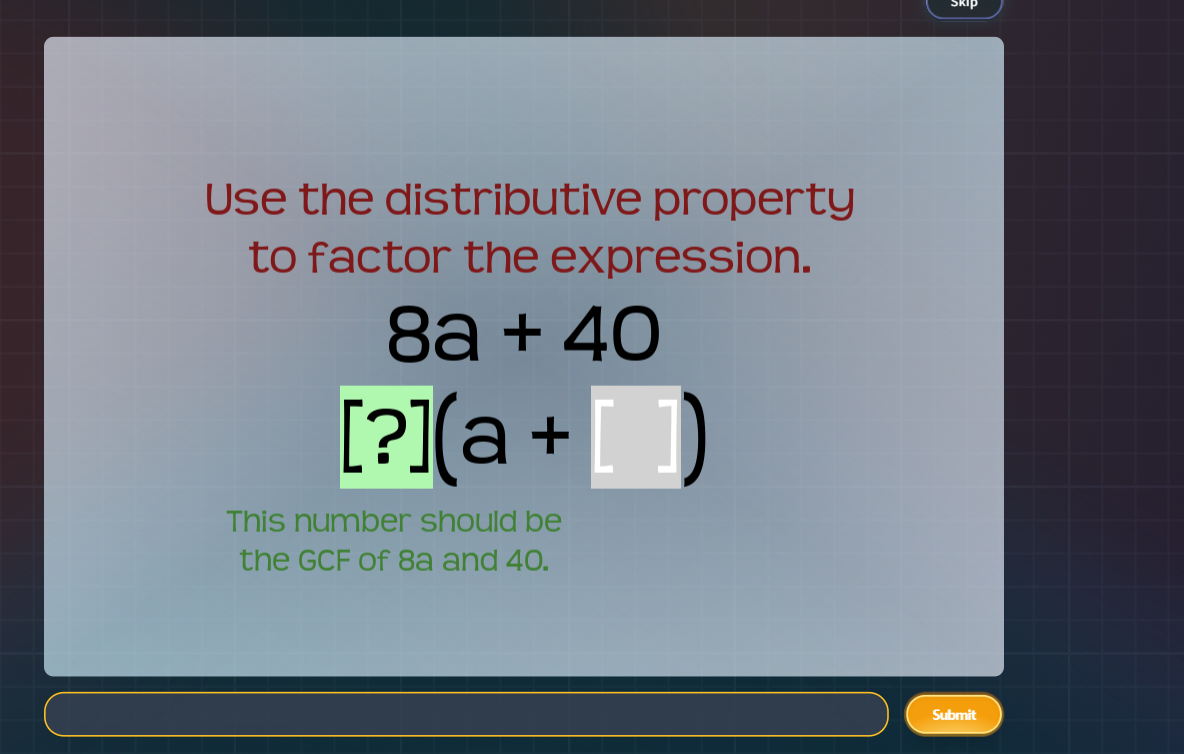
Use the distributive property to factor the expression 8a + 40. This number should be the GCF of 8a and 40.
Understand the Problem
The question asks to use the distributive property to factor the expression '8a + 40' and indicates that the number should be the greatest common factor (GCF) of 8a and 40.
Answer
The factored form is \(8(a + 5)\).
Answer for screen readers
The factored expression is (8(a + 5)).
Steps to Solve
- Identify the Greatest Common Factor (GCF)
To factor the expression (8a + 40), we need to find the GCF of the coefficients (8) and (40). The factors of (8) are (1, 2, 4, 8), and the factors of (40) are (1, 2, 4, 5, 8, 10, 20, 40). The GCF is the largest factor common to both sets, which is (8).
- Factor out the GCF
Next, we rewrite the expression by factoring out (8):
[ 8a + 40 = 8(a + \frac{40}{8}) ]
- Simplify the expression inside the parentheses
Calculating (\frac{40}{8}) gives us (5):
[ 8(a + 5) ]
Thus, the expression factored using the distributive property is (8(a + 5)).
The factored expression is (8(a + 5)).
More Information
Factoring using the distributive property helps in simplifying expressions. The GCF is a crucial concept in algebra, making it easier to work with polynomials.
Tips
- Forgetting to find the GCF correctly.
- Not simplifying the expression inside the parentheses.
- Misplacing the original terms in the expression after factoring.
AI-generated content may contain errors. Please verify critical information