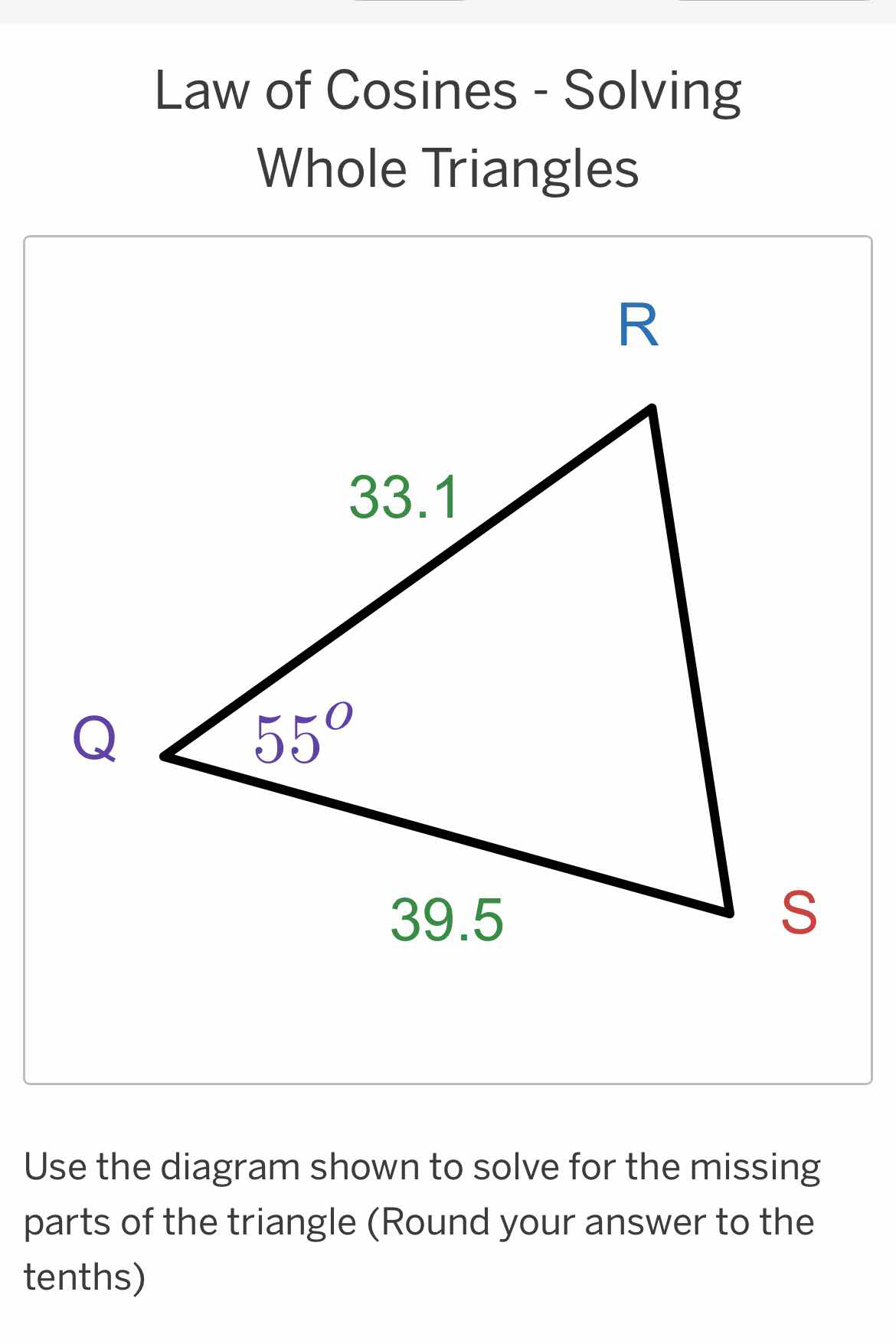
Use the diagram shown to solve for the missing parts of the triangle. Round your answer to the tenths.

Steps to Solve

1. Identify the known values We have a triangle with the following known values:

• Side ( QR = 39.5 )
• Side ( RS = 33.1 )
• Angle ( Q = 55^\circ )

2. Use the Law of Cosines to find side ( QS ) The Law of Cosines states that: $$ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) $$

Where:

• ( c ) is the side opposite angle ( C )
• ( a ) and ( b ) are the other two sides

For our triangle, we can set:

• ( a = QR = 39.5 )
• ( b = RS = 33.1 )
• ( C = 55^\circ )
• ( c = QS )

Now we can plug the values into the formula to find ( QS ): $$ QS^2 = 39.5^2 + 33.1^2 - 2 \cdot 39.5 \cdot 33.1 \cdot \cos(55^\circ) $$

3. Calculate ( QS^2 ) Now we compute the respective squares and the cosine: $$ QS^2 = 1560.25 + 1095.61 - 2 \cdot 39.5 \cdot 33.1 \cdot 0.5736 $$

Calculating further:

1. Calculate the multiplication: ( 2 \cdot 39.5 \cdot 33.1 \cdot 0.5736 )

2. Deduct from the sum of squares to find ( QS^2 ).

3. Calculate side ( QS ) Take the square root of ( QS^2 ): $$ QS = \sqrt{QS^2} $$

4. Determine the remaining angles using the Law of Sines Now that we have ( QS ), we can determine the angles ( R ) and ( S ) using the Law of Sines: $$ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} $$

Using:

• ( a = RS = 33.1 )
• ( b = QS )
• ( c = QR = 39.5 )
• ( A = 55^\circ )

Finding angle ( R ): $$ \frac{39.5}{\sin(R)} = \frac{33.1}{\sin(55^\circ)} $$

6. Calculate angle ( R ) Rearranging gives: $$ \sin(R) = \frac{39.5 \cdot \sin(55^\circ)}{33.1} $$

Finally, apply the inverse sine: $$ R = \arcsin(\frac{39.5 \cdot \sin(55^\circ)}{33.1}) $$

7. Find angle ( S ) For angle ( S ), use: $$ S = 180^\circ - R - 55^\circ $$