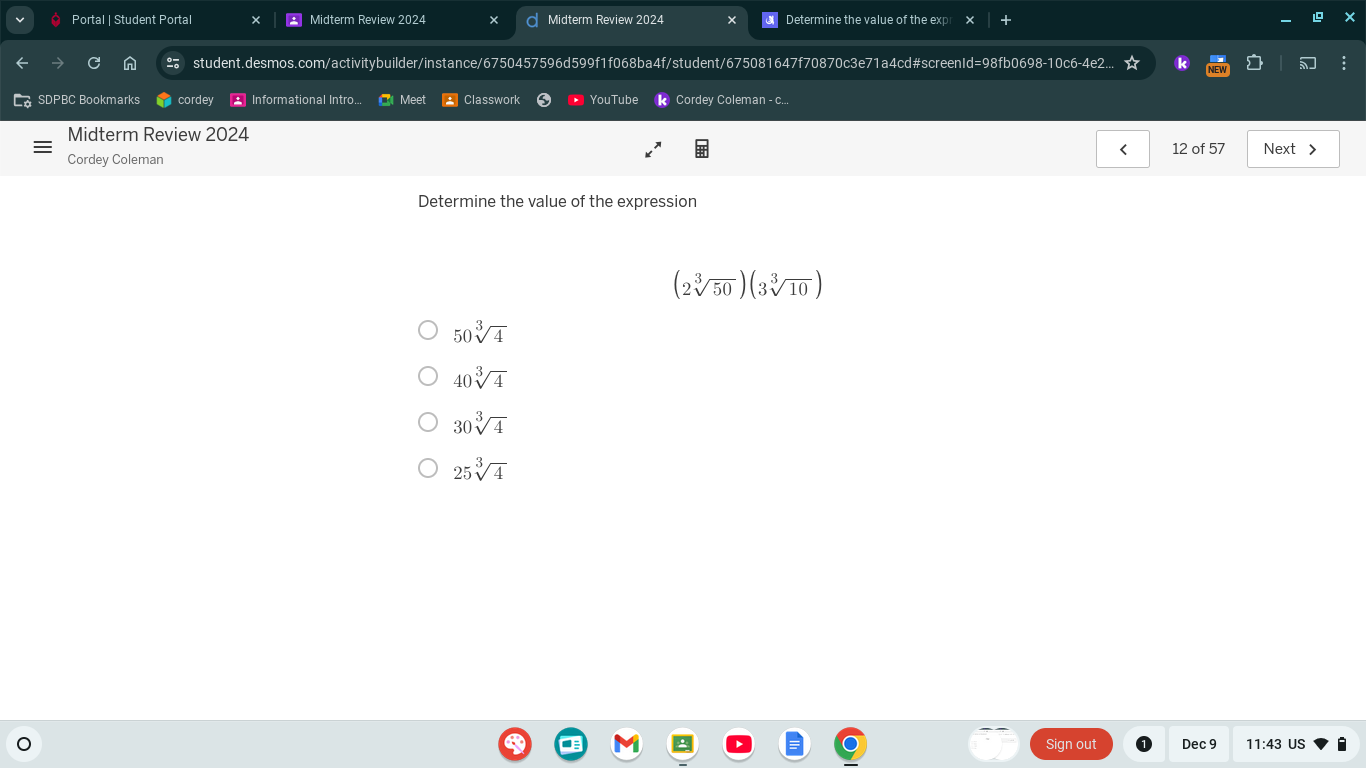
Determine the value of the expression (2^3√50)(3^3√10)
Understand the Problem
The question is asking for the value of the expression (2^3√50)(3^3√10). The solution will involve simplifying the expression using properties of exponents and square roots.
Answer
The answer is \( 2160 \sqrt{5} \).
Answer for screen readers
The final answer is ( 2160 \sqrt{5} ).
Steps to Solve
- Simplify the Square Roots
Start by simplifying each square root in the expression.
The quantity inside the first square root is $50$: $$ \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} $$
The quantity inside the second square root is $10$: $$ \sqrt{10} = \sqrt{10} $$
- Substitute the Simplified Roots
Replace the square roots in the expression: $$ (2^3 \cdot 5\sqrt{2})(3^3 \cdot \sqrt{10}) $$
- Calculate the Constants and Combine
Calculate the constants: $$ 2^3 = 8 \quad \text{and} \quad 3^3 = 27 $$
Now substitute them back into the expression: $$ (8 \cdot 5\sqrt{2})(27 \cdot \sqrt{10}) = 40\sqrt{2} \cdot 27\sqrt{10} $$
- Multiply the Constants and Square Roots
Now multiply the constants together and the square roots: $$ 40 \cdot 27 = 1080 $$
For the square roots, we have: $$ \sqrt{2} \cdot \sqrt{10} = \sqrt{20} = \sqrt{4 \cdot 5} = 2\sqrt{5} $$
Putting it all together: $$ 1080 \cdot 2\sqrt{5} = 2160\sqrt{5} $$
- Final Expression
The final expression is: $$ 2160 \sqrt{5} $$
The final answer is ( 2160 \sqrt{5} ).
More Information
The result ( 2160\sqrt{5} ) combines the constants and square roots from the original expression. It illustrates how manipulating square roots and powers can simplify complex expressions.
Tips
- Confusing the square roots, especially in multiplying the expressions.
- Forgetting to apply the properties of exponents correctly when combining the constants.
- Not simplifying the square roots properly, which can lead to incorrect bold answers.
AI-generated content may contain errors. Please verify critical information