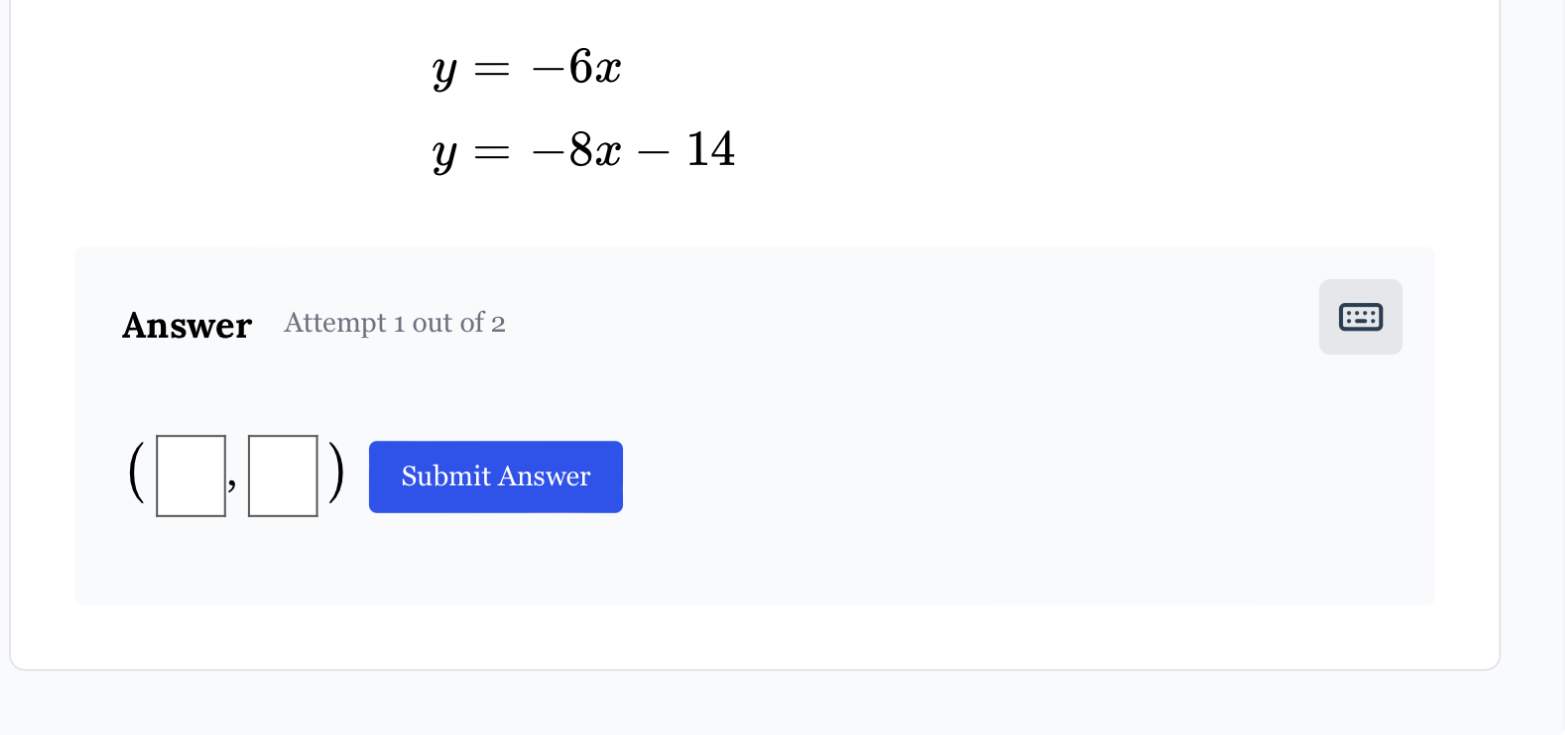
y = -6x; y = -8x - 14
Understand the Problem
The question involves solving a system of linear equations to find the intersection point of the two lines represented by the equations. This intersection point will yield the values of x and y.
Answer
$(-7, 42)$
Answer for screen readers
The intersection point of the two lines is $(-7, 42)$.
Steps to Solve
- Set the equations equal to each other
Since both equations equal $y$, we can set them equal to each other:
$$ -6x = -8x - 14 $$
- Isolate the variable (x)
To isolate (x), we add (8x) to both sides:
$$ -6x + 8x = -14 $$
This simplifies to:
$$ 2x = -14 $$
- Solve for (x)
Now, divide both sides by (2):
$$ x = \frac{-14}{2} $$
So,
$$ x = -7 $$
- Substitute (x) back into one of the original equations
We'll use the first equation (y = -6x):
$$ y = -6(-7) $$
This simplifies to:
$$ y = 42 $$
- Write the solution as a coordinate point
The intersection point of the two lines is therefore:
$$ (x, y) = (-7, 42) $$
The intersection point of the two lines is $(-7, 42)$.
More Information
This point represents the values of (x) and (y) where the two lines intersect on a graph. This method is commonly used in algebra to solve systems of linear equations.
Tips
- Forgetting to combine like terms when isolating the variable.
- Miscalculating the value of (y) after substituting (x).
- Misreading the question and inaccurately determining the lines' intersection.
AI-generated content may contain errors. Please verify critical information