Use the appropriate compound angle formula to determine the exact value of each expression. a) sin(π + π/6) b) cos(π - π/4) c) tan(π/4 + π) d) sin(-π/2 + π/3) e) tan(π/3 - π/6) f)... Use the appropriate compound angle formula to determine the exact value of each expression. a) sin(π + π/6) b) cos(π - π/4) c) tan(π/4 + π) d) sin(-π/2 + π/3) e) tan(π/3 - π/6) f) cos(π/2 + π/3)
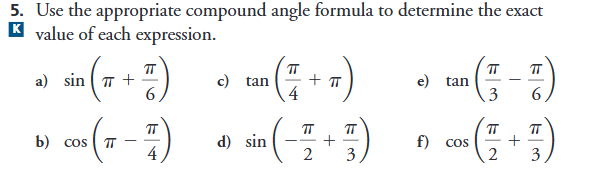
Understand the Problem
The question asks to apply the appropriate compound angle formulas to find the exact values of various trigonometric expressions involving sine, cosine, and tangent functions.
Answer
a) \( -\frac{1}{2} \) b) \( -\frac{\sqrt{2}}{2} \) c) \( 1 \) d) \( -\frac{1}{2} \) e) \( \frac{1}{\sqrt{3}} \) f) \( -\frac{\sqrt{3}}{2} \)
Answer for screen readers
a) ( -\frac{1}{2} )
b) ( -\frac{\sqrt{2}}{2} )
c) ( 1 )
d) ( -\frac{1}{2} )
e) ( \frac{1}{\sqrt{3}} )
f) ( -\frac{\sqrt{3}}{2} )
Steps to Solve
- Identify the appropriate formula for sine To find ( \sin\left(\pi + \frac{\pi}{6}\right) ), we can use the sine addition formula: $$ \sin(a + b) = \sin a \cos b + \cos a \sin b $$
Here, ( a = \pi ) and ( b = \frac{\pi}{6} ).
Calculate:
- ( \sin(\pi) = 0 )
- ( \cos(\pi) = -1 )
- ( \sin\left(\frac{\pi}{6}\right) = \frac{1}{2} )
- ( \cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2} )
Then substitute into the formula: $$ \sin\left(\pi + \frac{\pi}{6}\right) = 0 \cdot \frac{\sqrt{3}}{2} + (-1) \cdot \frac{1}{2} = -\frac{1}{2} $$
- Determine cosine using subtraction formula For ( \cos\left(\pi - \frac{\pi}{4}\right) ), use the cosine subtraction formula: $$ \cos(a - b) = \cos a \cos b + \sin a \sin b $$
Here, ( a = \pi ) and ( b = \frac{\pi}{4} ).
Calculate:
- ( \cos(\pi) = -1 )
- ( \sin(\pi) = 0 )
- ( \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} )
- ( \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} )
Substitute: $$ \cos\left(\pi - \frac{\pi}{4}\right) = (-1) \cdot \frac{\sqrt{2}}{2} + 0 \cdot \frac{\sqrt{2}}{2} = -\frac{\sqrt{2}}{2} $$
- Calculate tangent for addition of angles For ( \tan\left(\frac{\pi}{4} + \pi\right) ): Use the tangent angle addition formula: $$ \tan(a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b} $$
Here, ( a = \frac{\pi}{4} ) and ( b = \pi ).
Calculate:
- ( \tan\left(\frac{\pi}{4}\right) = 1 )
- ( \tan(\pi) = 0 )
Then, $$ \tan\left(\frac{\pi}{4} + \pi\right) = \frac{1 + 0}{1 - 1 \cdot 0} = 1 $$
- Determine sine for angle combination For ( \sin\left(-\frac{\pi}{2} + \frac{\pi}{3}\right) ): First, convert using the sine subtraction formula: $$ \sin(a - b) = \sin a \cos b - \cos a \sin b $$
Here, ( a = -\frac{\pi}{2} ) and ( b = \frac{\pi}{3} ).
Calculate:
- ( \sin\left(-\frac{\pi}{2}\right) = -1 )
- ( \cos\left(-\frac{\pi}{2}\right) = 0 )
- ( \cos\left(\frac{\pi}{3}\right) = \frac{1}{2} )
- ( \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2} )
Substitute: $$ \sin\left(-\frac{\pi}{2} + \frac{\pi}{3}\right) = -1 \cdot \frac{1}{2} - 0 \cdot \frac{\sqrt{3}}{2} = -\frac{1}{2} $$
- Find tangent for subtraction For ( \tan\left(\frac{\pi}{3} - \frac{\pi}{6}\right) ): Use the tangent subtraction formula: $$ \tan(a - b) = \frac{\tan a - \tan b}{1 + \tan a \tan b} $$
Here, ( a = \frac{\pi}{3} ) and ( b = \frac{\pi}{6} ).
Calculate:
- ( \tan\left(\frac{\pi}{3}\right) = \sqrt{3} )
- ( \tan\left(\frac{\pi}{6}\right) = \frac{1}{\sqrt{3}} )
Substitute: $$ \tan\left(\frac{\pi}{3} - \frac{\pi}{6}\right) = \frac{\sqrt{3} - \frac{1}{\sqrt{3}}}{1 + \sqrt{3} \cdot \frac{1}{\sqrt{3}}} = \frac{\sqrt{3} - \frac{1}{\sqrt{3}}}{2} = \frac{\frac{3}{\sqrt{3}} - \frac{1}{\sqrt{3}}}{2} = \frac{\frac{2}{\sqrt{3}}}{2} = \frac{1}{\sqrt{3}} $$
- Calculate cosine for angle addition For ( \cos\left(\frac{\pi}{2} + \frac{\pi}{3}\right) ): Use the cosine addition formula: $$ \cos(a + b) = \cos a \cos b - \sin a \sin b $$
Here, ( a = \frac{\pi}{2} ) and ( b = \frac{\pi}{3} ).
Calculate:
- ( \cos\left(\frac{\pi}{2}\right) = 0 )
- ( \sin\left(\frac{\pi}{2}\right) = 1 )
- ( \cos\left(\frac{\pi}{3}\right) = \frac{1}{2} )
- ( \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2} )
Substitute: $$ \cos\left(\frac{\pi}{2} + \frac{\pi}{3}\right) = 0 \cdot \frac{1}{2} - 1 \cdot \frac{\sqrt{3}}{2} = -\frac{\sqrt{3}}{2} $$
a) ( -\frac{1}{2} )
b) ( -\frac{\sqrt{2}}{2} )
c) ( 1 )
d) ( -\frac{1}{2} )
e) ( \frac{1}{\sqrt{3}} )
f) ( -\frac{\sqrt{3}}{2} )
More Information
These problems utilize the sine and cosine addition and subtraction formulas, showing how angles can be manipulated to find exact trigonometric values. Each function is evaluated based on fundamental properties of trigonometric functions and their respective angle values.
Tips
- Mistaking sine and cosine values for angles. Always check the unit circle for the correct values.
- Forgetting that tangent can be simplified differently based on angle identities.
- Incorrectly using the formulas; ensure the proper formula (addition or subtraction) is used based on the problem.
AI-generated content may contain errors. Please verify critical information