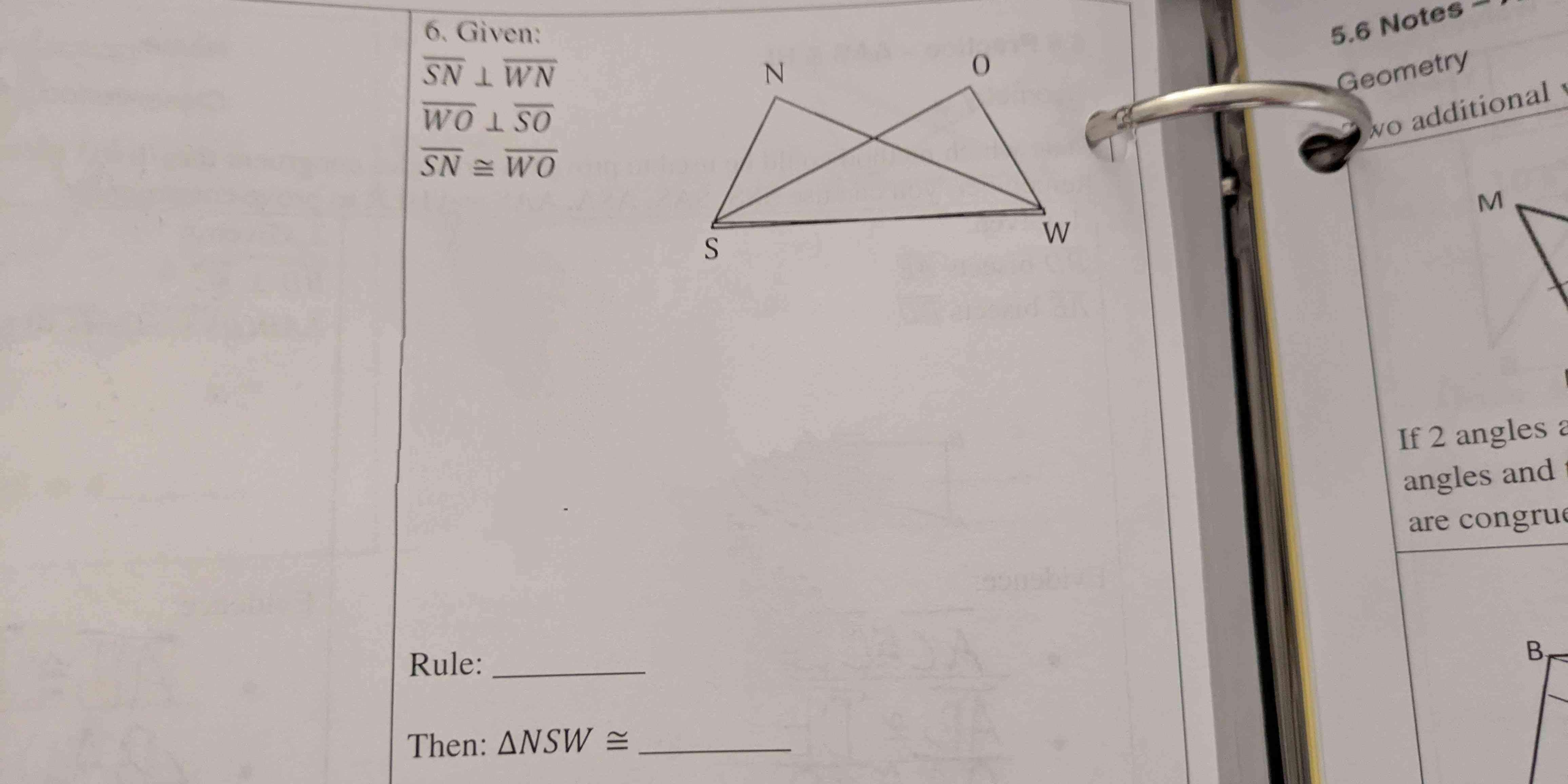
If SN is perpendicular to NW, WO is perpendicular to SO, and SN is congruent to WO, what rule can be used to prove that triangle NSW is congruent to triangle OSW?
Understand the Problem
The question is asking to determine a geometric rule for the congruence of triangles based on the given conditions involving right angles and congruent segments. We will apply the properties of triangles and the relationships between angles and sides to solve it.
Answer
The rule is \( \triangle SNW \cong \triangle WOS \).
Answer for screen readers
Rule: ( \triangle SNW \cong \triangle WOS )
Steps to Solve
- Identify Given Information
The problem states the following:
- ( SN \perp WN ): Segment ( SN ) is perpendicular to segment ( WN ).
- ( WO \perp SO ): Segment ( WO ) is perpendicular to segment ( SO ).
- ( SN \cong WO ): Segment ( SN ) is congruent to segment ( WO ).
- Analyze the Triangles
From the given information, we can see that there are two right triangles formed:
- Triangle ( \triangle SNW )
- Triangle ( \triangle WOS )
- Apply the Right Triangle Congruence Theorem
Since both triangles have:
- One right angle (from the perpendicular segments),
- A pair of congruent sides (i.e., ( SN \cong WO )),
We can use the Hypotenuse-Leg (HL) Theorem which states that if a right triangle has a hypotenuse and one leg that are congruent to the corresponding parts of another right triangle, then the two triangles are congruent.
- Formulate the Congruence Rule
Because we established that:
- ( \angle SNW \equiv \angle WOS ) (right angles)
- ( SN \cong WO ) (given)
The triangles ( \triangle SNW ) and ( \triangle WOS ) are congruent.
The rule can be stated as: Rule: ( \triangle SNW \cong \triangle WOS )
Rule: ( \triangle SNW \cong \triangle WOS )
More Information
This conclusion is derived from the properties of right triangles and the Hypotenuse-Leg congruence theorem, which is particularly useful in problems involving right angles.
Tips
Common mistakes include:
- Forgetting to note that the given segments are perpendicular, which is crucial for triangle congruence.
- Assuming that two triangles are congruent just because they have two sides the same length without also considering the angles.
AI-generated content may contain errors. Please verify critical information