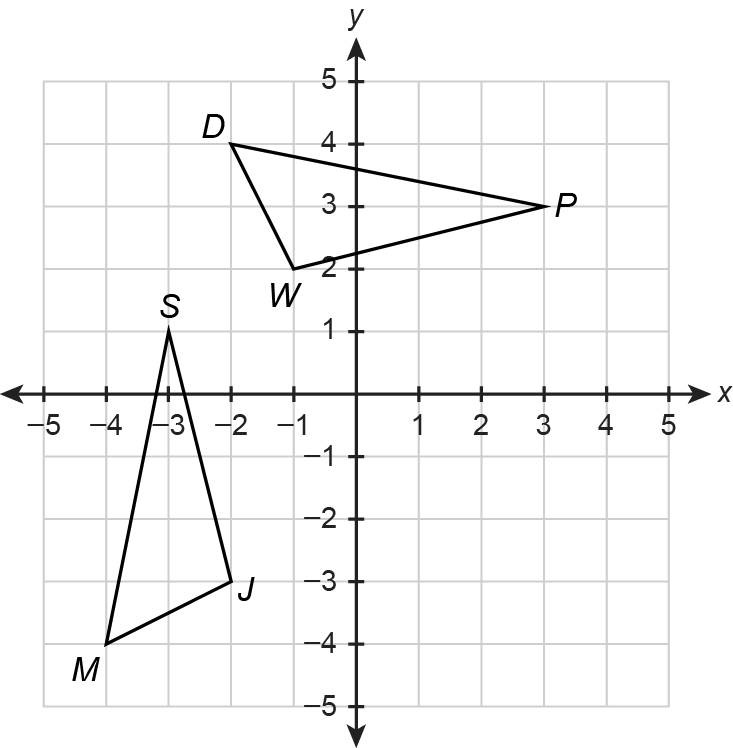
Use rigid motions to explain whether the triangles in the figure are congruent. Be sure to describe specific rigid motions in your explanation.

Steps to Solve

1. Identify the Vertices of Each Triangle

   For triangle DPW, the vertices are:

   • ( D(0, 4) )
   • ( P(3, 4) )
   • ( W(0, 2) )

   For triangle SMJ, the vertices are:

   • ( S(-2, -3) )
   • ( M(-3, -5) )
   • ( J(-1, -5) )

2. Calculate the Side Lengths of Each Triangle

   Use the distance formula ( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ).

   For triangle DPW:

   • ( DP = \sqrt{(3 - 0)^2 + (4 - 4)^2} = \sqrt{9} = 3 )
   • ( PW = \sqrt{(3 - 0)^2 + (4 - 2)^2} = \sqrt{(3)^2 + (2)^2} = \sqrt{13} )
   • ( WD = \sqrt{(0 - 0)^2 + (2 - 4)^2} = \sqrt{4} = 2 )

   For triangle SMJ:

   • ( SM = \sqrt{(-3 + 2)^2 + (-5 + 3)^2} = \sqrt{1 + 4} = \sqrt{5} )
   • ( MJ = \sqrt{(-3 + 1)^2 + (-5 + 5)^2} = \sqrt{4} = 2 )
   • ( SJ = \sqrt{(-1 + 2)^2 + (-5 + 3)^2} = \sqrt{1 + 4} = \sqrt{5} )

3. Compare Side Lengths

   From the calculated lengths:

   • Triangle DPW has sides ( 3, \sqrt{13}, 2 )
   • Triangle SMJ has sides ( \sqrt{5}, 2, \sqrt{5} )

   Since the sets of side lengths are different, the triangles have different side lengths.

4. Conclusion on Congruence

   Since the triangles have different side lengths, they cannot be congruent. Therefore, no rigid motion can map triangle SMJ onto triangle DPW.