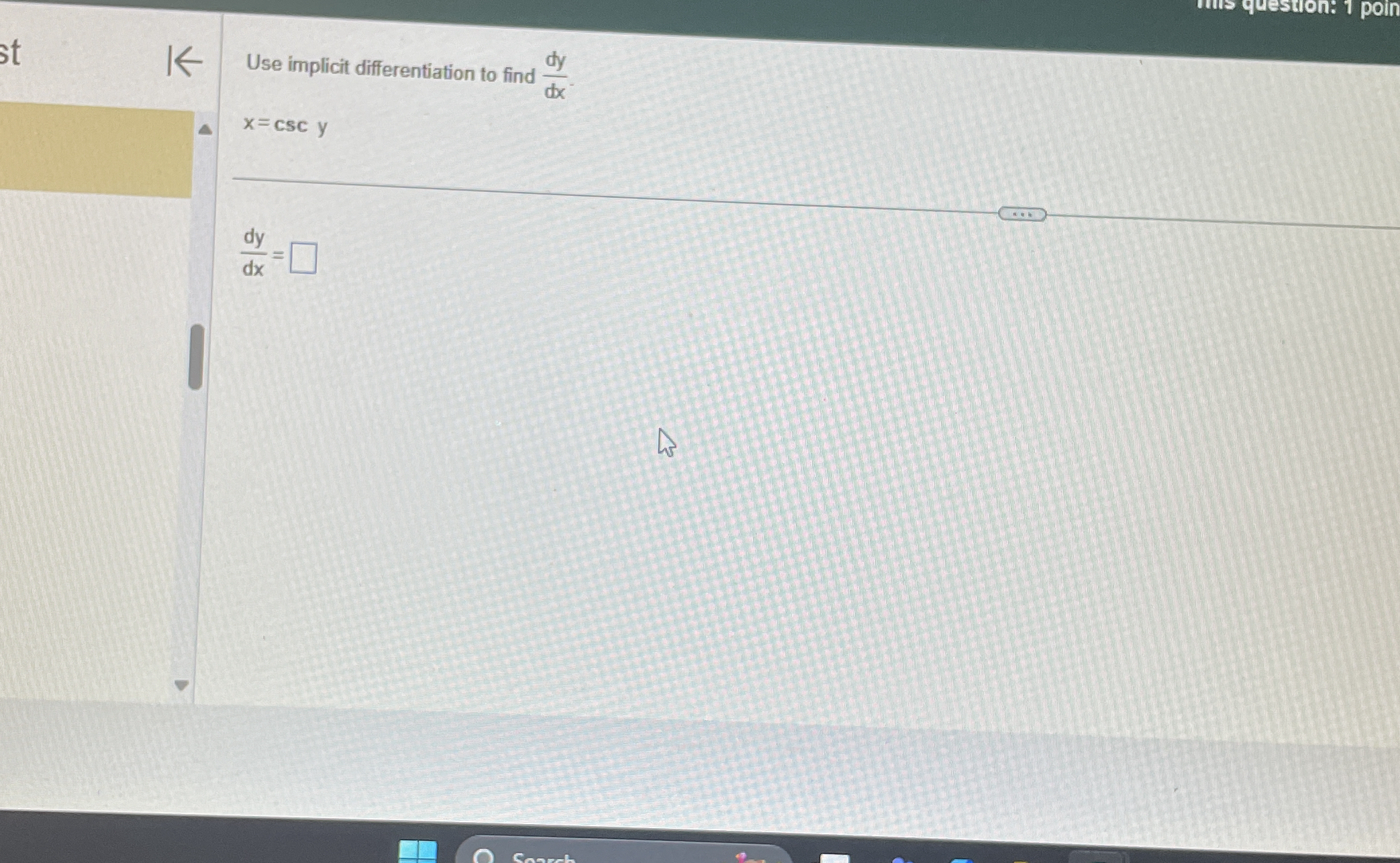
Use implicit differentiation to find dy/dx for the equation x = csc(y).
Understand the Problem
The question is asking for the implicit differentiation of the equation x = csc(y) to find dy/dx. This involves applying the rules of differentiation, including the chain rule and the properties of the cosecant function.
Answer
$$ \frac{dy}{dx} = -\frac{\sin^2(y)}{\cos(y)} $$
Answer for screen readers
The final answer for ( \frac{dy}{dx} ) is:
$$ \frac{dy}{dx} = -\frac{\sin^2(y)}{\cos(y)} $$
Steps to Solve
- Differentiate both sides with respect to x
We start with the equation:
$$ x = \csc(y) $$
Now, differentiate both sides with respect to $x$. The left side differentiates to $1$. For the right side, we use the chain rule:
$$ \frac{d}{dx}(\csc(y)) = -\csc(y)\cot(y) \frac{dy}{dx} $$
This gives us the equation:
$$ 1 = -\csc(y) \cot(y) \frac{dy}{dx} $$
- Isolate ( \frac{dy}{dx} )
Now, we want to solve for ( \frac{dy}{dx} ). Rearranging the equation gives:
$$ \frac{dy}{dx} = -\frac{1}{\csc(y) \cot(y)} $$
- Simplify the expression
To simplify, recall that $\csc(y) = \frac{1}{\sin(y)}$ and $\cot(y) = \frac{\cos(y)}{\sin(y)}$. Substituting these into the equation gives:
$$ \frac{dy}{dx} = -\frac{1}{\frac{1}{\sin(y)} \cdot \frac{\cos(y)}{\sin(y)}} $$
This simplifies further to:
$$ \frac{dy}{dx} = -\frac{\sin^2(y)}{\cos(y)} $$
The final answer for ( \frac{dy}{dx} ) is:
$$ \frac{dy}{dx} = -\frac{\sin^2(y)}{\cos(y)} $$
More Information
Implicit differentiation is a useful technique when dealing with relationships between variables that are not easily separable. This method allows us to find derivatives even when the equation is not explicitly solved for one variable in terms of the other.
Tips
- Forgetting to apply the chain rule correctly when differentiating a function of (y).
- Failing to isolate ( \frac{dy}{dx} ) before simplifying.
- Not remembering the identities of trigonometric functions, which can simplify the differentiation process.
AI-generated content may contain errors. Please verify critical information