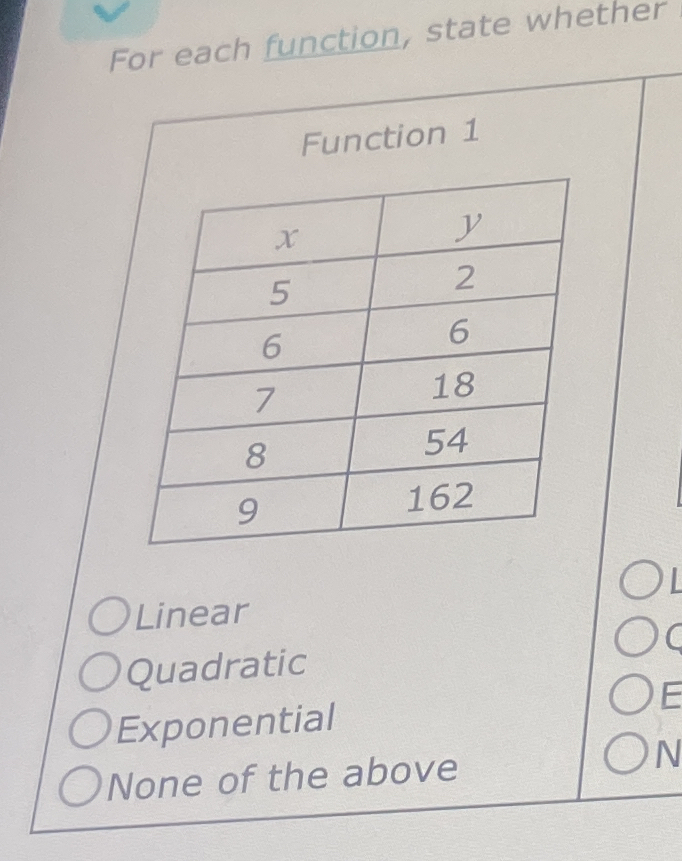
For each function, state whether the function is linear, quadratic, exponential, or none of the above based on the given (x, y) values.

Steps to Solve

1. Identify the pattern of y-values

   We need to examine if there is a consistent relationship between the x-values and y-values. Let's look at the y-values:

   • When $x = 5$, $y = 2$
   • When $x = 6$, $y = 6$
   • When $x = 7$, $y = 18$
   • When $x = 8$, $y = 54$
   • When $x = 9$, $y = 162$

2. Calculate the ratio of consecutive y-values

   This step helps in identifying if the pattern is exponential or not. We will calculate the ratio of consecutive y-values.

   For example:

   • $\frac{y(6)}{y(5)} = \frac{6}{2} = 3$
   • $\frac{y(7)}{y(6)} = \frac{18}{6} = 3$
   • $\frac{y(8)}{y(7)} = \frac{54}{18} = 3$
   • $\frac{y(9)}{y(8)} = \frac{162}{54} = 3$

   Since the ratio is consistent (3), we can conclude that the relationship is exponential.

3. Express the relationship of the function

   The relationship can be expressed as $y = 2 \cdot 3^{(x-5)}$, showing that it represents an exponential function where the base is 3 and the exponent is dependent on the value of x.