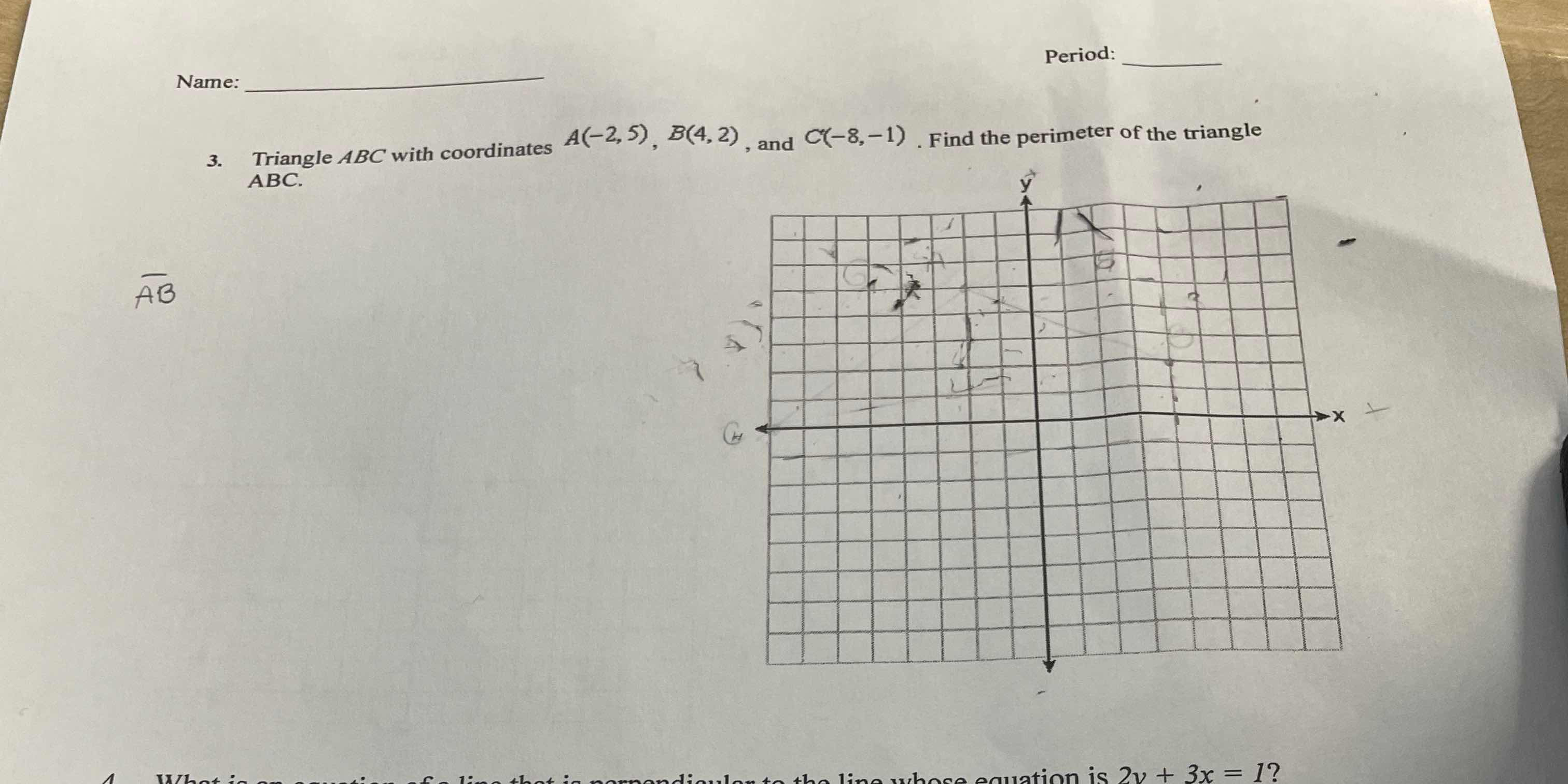
Triangle ABC with coordinates A(-2, 5), B(4, 2), and C(-8, -1). Find the perimeter of the triangle ABC.

Understand the Problem

The question is asking to calculate the perimeter of triangle ABC, which is defined by the coordinates of its vertices A(-2, 5), B(4, 2), and C(-8, -1). To solve this, we need to find the lengths of the sides of the triangle using the distance formula and then sum those lengths to find the perimeter.

Answer

The perimeter of triangle ABC is $3\sqrt{5} + 3\sqrt{17} + 6\sqrt{2}$.

Steps to Solve

Calculate the length of side AB Use the distance formula, which is given by: $$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$ For points A(-2, 5) and B(4, 2): $$ AB = \sqrt{(4 - (-2))^2 + (2 - 5)^2} = \sqrt{(4 + 2)^2 + (2 - 5)^2} = \sqrt{6^2 + (-3)^2} = \sqrt{36 + 9} = \sqrt{45} = 3\sqrt{5} $$
Calculate the length of side BC Again use the distance formula for points B(4, 2) and C(-8, -1): $$ BC = \sqrt{(-8 - 4)^2 + (-1 - 2)^2} = \sqrt{(-12)^2 + (-3)^2} = \sqrt{144 + 9} = \sqrt{153} = 3\sqrt{17} $$
Calculate the length of side CA Use the distance formula for points C(-8, -1) and A(-2, 5): $$ CA = \sqrt{(-2 - (-8))^2 + (5 - (-1))^2} = \sqrt{(6)^2 + (6)^2} = \sqrt{36 + 36} = \sqrt{72} = 6\sqrt{2} $$
Calculate the perimeter of triangle ABC The perimeter P can be calculated as follows: $$ P = AB + BC + CA = 3\sqrt{5} + 3\sqrt{17} + 6\sqrt{2} $$

The perimeter of triangle ABC is given by: $$ P = 3\sqrt{5} + 3\sqrt{17} + 6\sqrt{2} $$

More Information

The perimeter represents the total distance around the triangle formed by points A, B, and C in the coordinate plane.

Tips

Forgetting to use parentheses: When substituting coordinates into the distance formula, it’s easy to forget parentheses, which can result in wrong calculations.
Misapplying the distance formula: Ensure that you correctly identify the coordinates of each vertex when plugging them into the formula.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!