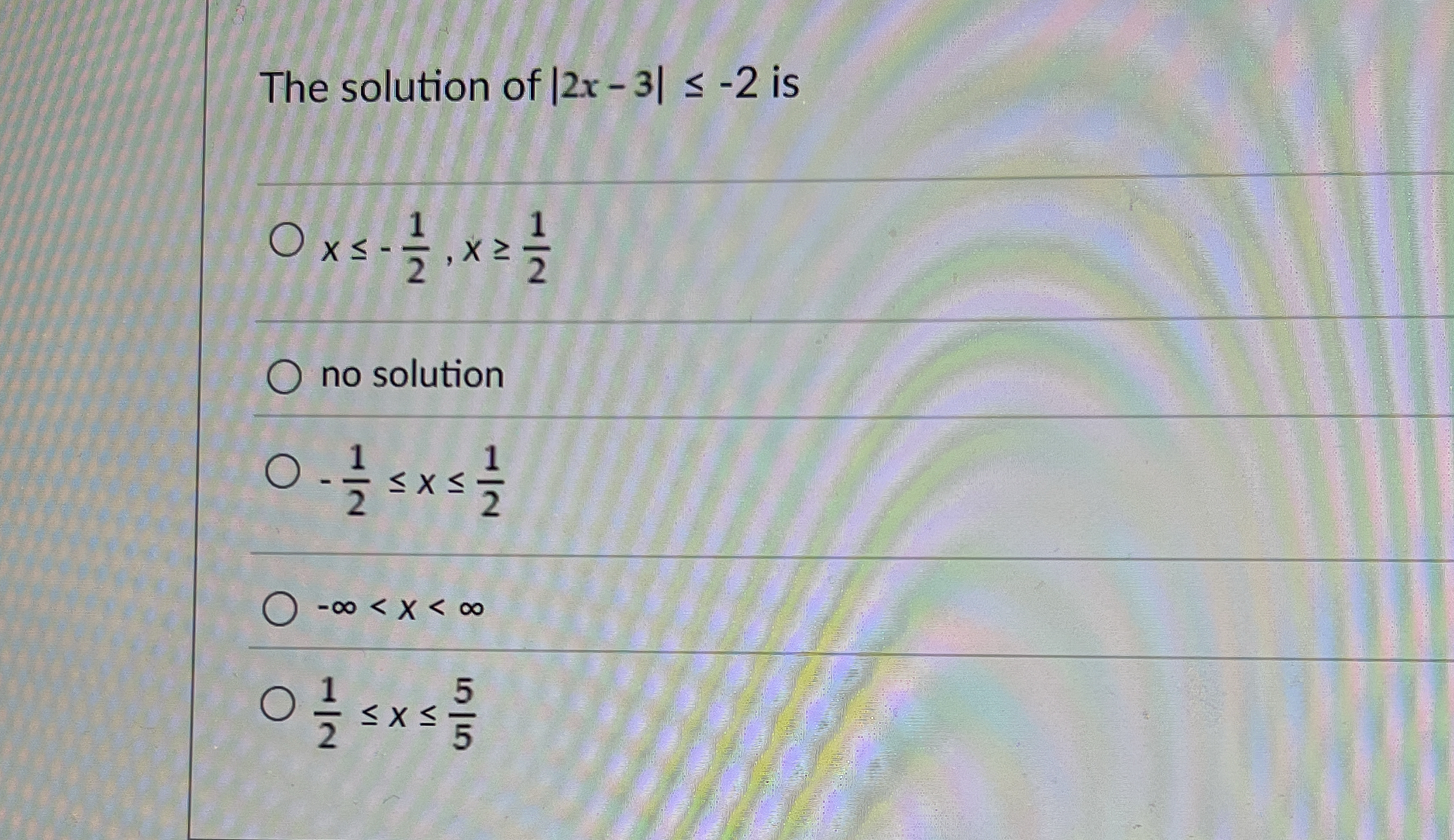
The solution of |2x - 3| ≤ -2 is
Understand the Problem
The question is asking for the solution set of the inequality involving the absolute value expression |2x - 3| ≤ -2. Specifically, it wants to determine what values of x satisfy this inequality.
Answer
no solution
Answer for screen readers
The answer is "no solution".
Steps to Solve
- Understanding Absolute Value Inequality
The inequality involves the absolute value $|2x - 3|$. Recall that the absolute value of a number is always non-negative (i.e., $\geq 0$). Therefore, the expression $|2x - 3| ≤ -2$ implies that we need to find when an absolute value is less than or equal to a negative number.
- Analyzing the Inequality
Since absolute values cannot be negative, we realize that $|2x - 3| ≤ -2$ has no solutions. The left side, which represents a distance, cannot be less than a negative value.
- Conclusion of No Solution
With this understanding, we conclude that the inequality has no valid solutions.
The answer is "no solution".
More Information
The concept that absolute values cannot be negative is fundamental in understanding inequalities involving absolute values. Thus, finding a non-existing solution reaffirms the properties of absolute values.
Tips
Certainly! A common mistake is assuming that the inequality can still yield valid x-values or misinterpreting the meaning of inequality involving an absolute value compared to a negative number.
AI-generated content may contain errors. Please verify critical information