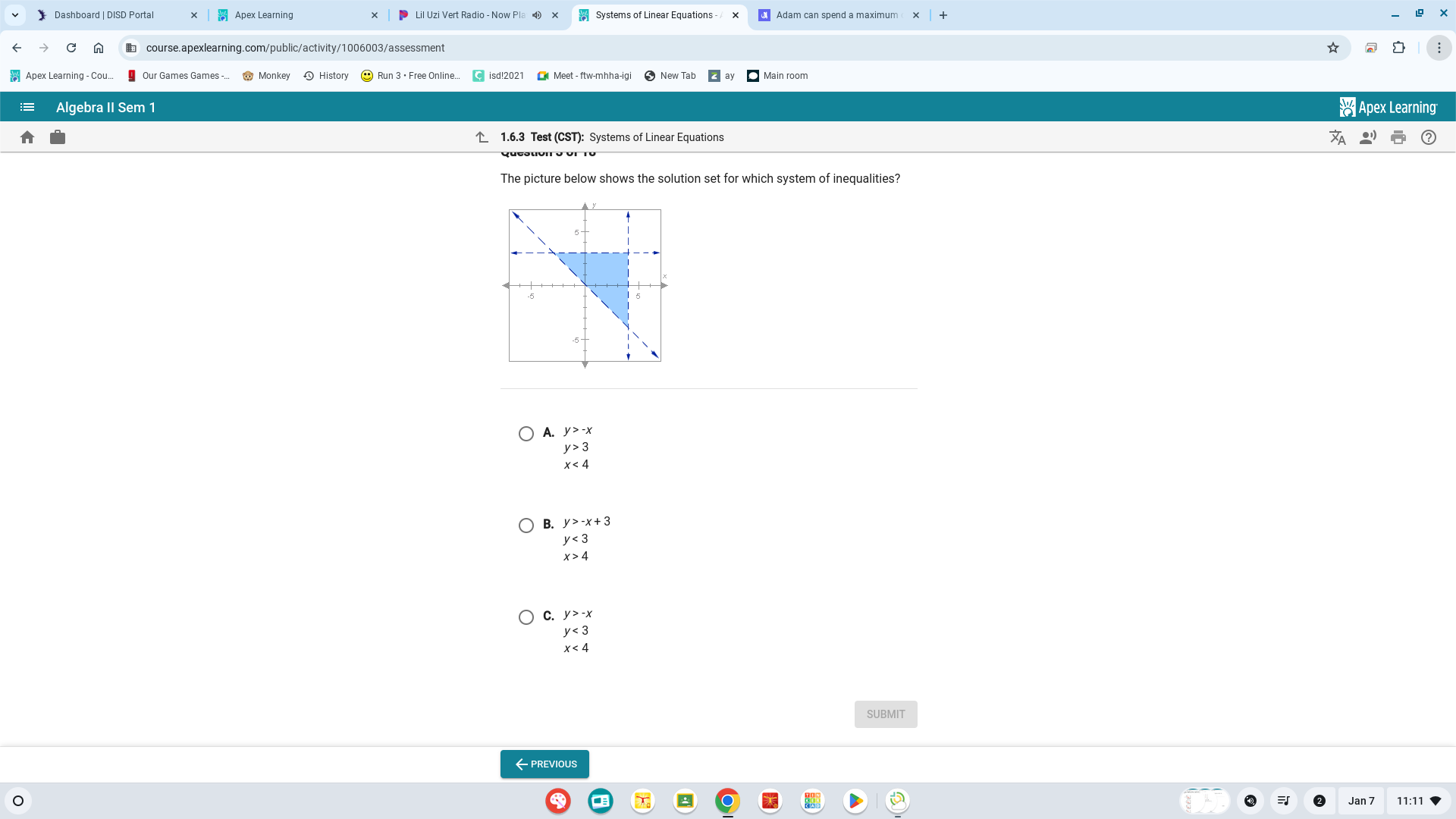
The picture below shows the solution set for which system of inequalities?
Understand the Problem
The question asks which system of inequalities corresponds to the shaded solution set shown in the provided graph. This requires analyzing the inequalities in the answer choices in relation to the region represented in the graph.
Answer
The answer is **C**: $y < -x$, $y < 3$, $x < 4$.
Answer for screen readers
The correct system of inequalities is:
$$ \begin{align*} y & < -x \ y & < 3 \ x & < 4 \end{align*} $$
Thus, the answer is C.
Steps to Solve
-
Identify the boundaries The graph displays the shaded region defined by two lines. The first line can be deduced as the boundary for $y = x$ because the shaded area lies below this line. The second boundary is horizontal and can represent $y = 3$, as it is dashed and indicates a limit.
-
Determine the inequalities The inequality for the first line will be $y < x$, indicating that the solution set is below the line. For the second line, since the shaded area is below it but does not include it, this can be expressed as $y < 3$.
-
Examine the x-value restriction Notice that the region is also limited on the right side, indicating that $x$ must be less than the line that appears to be vertical and at $x = 4$. This suggests the inequality $x < 4$.
-
Combine the inequalities Thus, the combined inequalities for the shaded region are: $$ \begin{align*} y & < x \ y & < 3 \ x & < 4 \end{align*} $$
-
Match with answer choices Now, we need to match the derived inequalities with the answer choices. The options are:
- A: $y < -x$, $y > 3$, $x < 4$
- B: $y < -x + 3$, $y < 3$, $x > 4$
- C: $y < -x$, $y < 3$, $x < 4$
After careful examination, we check which option corresponds to our derived inequalities.
The correct system of inequalities is:
$$ \begin{align*} y & < -x \ y & < 3 \ x & < 4 \end{align*} $$
Thus, the answer is C.
More Information
In this problem, the inequalities are derived from the lines shown in the graph. The dashed lines indicate that the boundaries are not part of the solution, leading to "less than" inequalities for the top line and the horizontal line.
Tips
- Mistaking dashed lines for solid lines and incorrectly including those boundaries in the inequalities.
- Confusing the direction of the inequalities (e.g., writing $y > x$ instead of $y < x$).
AI-generated content may contain errors. Please verify critical information