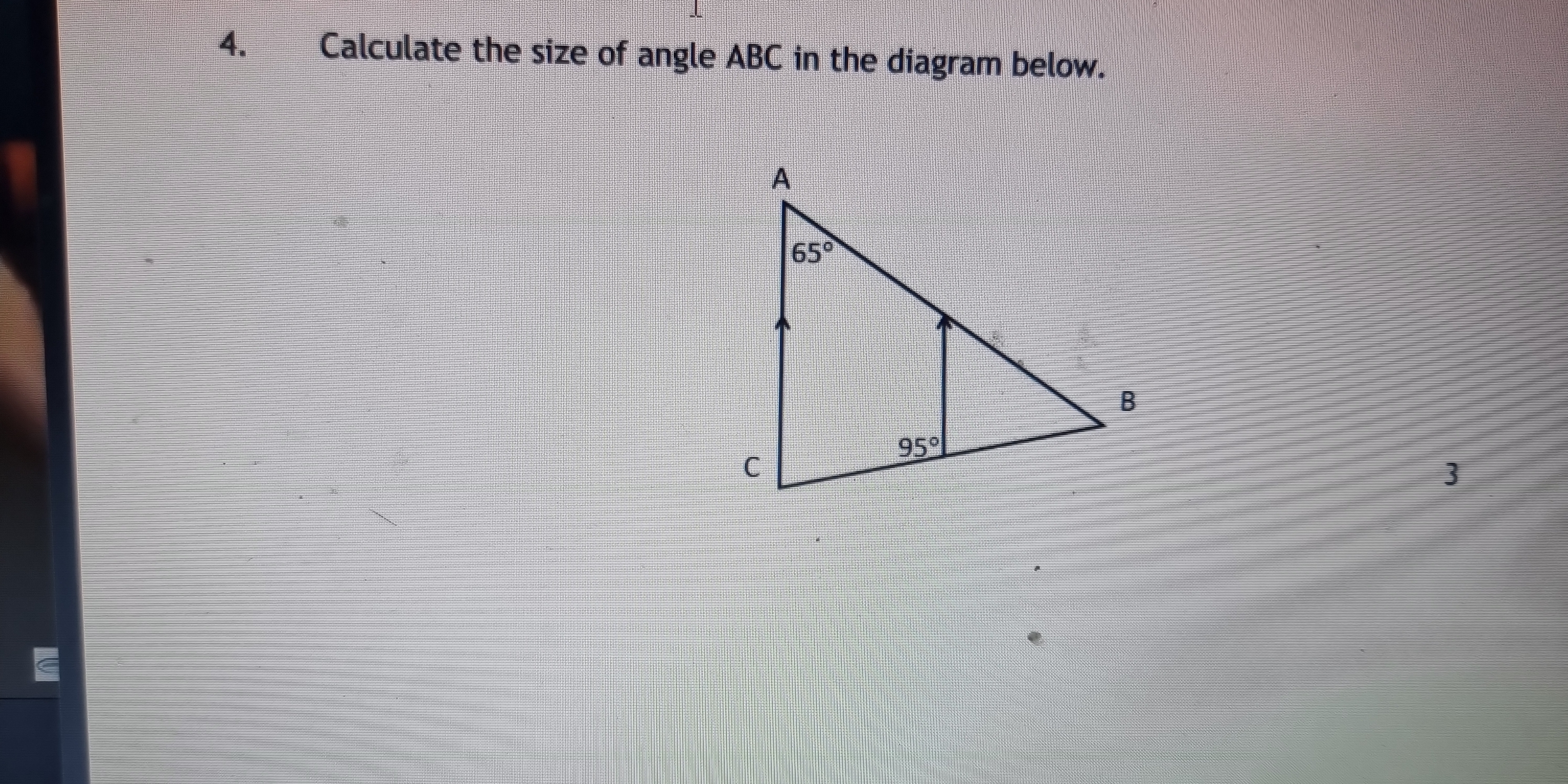
Calculate the size of angle ABC in the diagram below.
Understand the Problem
The question is asking to calculate the size of angle ABC in a triangle where two angles (65° and 95°) are already provided. We will solve it by applying the property of angles in a triangle, which states that the sum of all angles in a triangle is 180°.
Answer
The size of angle ABC is $20^\circ$.
Answer for screen readers
The size of angle ABC is $20^\circ$.
Steps to Solve
- Identify the angles in the triangle
We have two angles given in triangle ABC:
- Angle A = 65°
- Angle C = 95°
- Use the triangle angle sum property
The sum of angles in a triangle is 180°. Therefore, we can express the sum of the angles in triangle ABC as: $$ \text{Angle A} + \text{Angle B} + \text{Angle C} = 180° $$
- Substitute the known angles
Substitute the values of Angle A and Angle C into the equation: $$ 65° + \text{Angle B} + 95° = 180° $$
- Combine the known angles
Combine the known angles (65° and 95°): $$ 160° + \text{Angle B} = 180° $$
- Solve for Angle B
Now, isolate Angle B: $$ \text{Angle B} = 180° - 160° = 20° $$
The size of angle ABC is $20^\circ$.
More Information
In any triangle, the angles always add up to 180°, which is a fundamental property of triangles. Knowing this allows us to find any missing angle as long as we have the other two.
Tips
- Ignoring the triangle angle sum property and adding angles incorrectly.
- Misplacing the angles (e.g., confusing which angle is which).
- Performing arithmetic incorrectly when subtracting from 180°.
AI-generated content may contain errors. Please verify critical information