The graph of function f is given below. On the same grid plot: a) -f(2x) - 3; b) 2f(x - 4); c) 1/2 f(-1/2 x) - 6; d) f^-1.
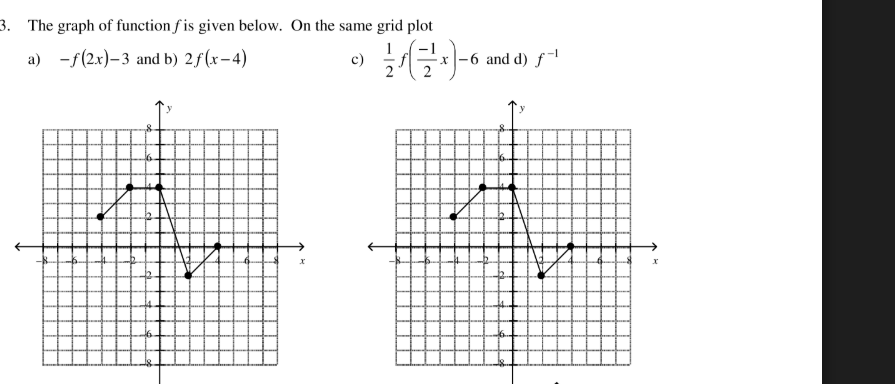
Understand the Problem
The question involves understanding the transformations of a given function f based on specific mathematical expressions. Each part a) through d) requires plotting the transformed functions on the same grid as the original function f.
Answer
The transformed functions are: a) $-f(2x) - 3$ b) $2f(x - 4)$ c) $\frac{1}{2}f\left(-\frac{1}{2}x\right) - 6$ d) $f^{-1}$
Answer for screen readers
The transformed functions are:
a) $-f(2x) - 3$
b) $2f(x - 4)$
c) $\frac{1}{2}f\left(-\frac{1}{2}x\right) - 6$
d) $f^{-1}$
Steps to Solve
-
Understanding the Transforms Each transformation represents a specific change to the function $f$. We need to analyze each part (a through d) individually to see how they affect the graph.
-
Transform for part (a): $-f(2x) - 3$
- The $f(2x)$ indicates a horizontal compression by a factor of 2.
- The $-f(2x)$ reflects the graph over the x-axis.
- The $-3$ translates it downward by 3 units.
-
Transform for part (b): $2f(x - 4)$
- The $f(x - 4)$ translates the graph to the right by 4 units.
- The $2f(x-4)$ stretches the graph vertically by a factor of 2.
-
Transform for part (c): $\frac{1}{2}f\left(-\frac{1}{2}x\right) - 6$
- The $-\frac{1}{2}x$ reflects the graph over the y-axis and compresses it horizontally by a factor of 2.
- The $\frac{1}{2}f$ part vertically compresses the graph by a factor of 2.
- The $-6$ translates it downward by 6 units.
-
Transform for part (d): $f^{-1}$
- The $f^{-1}$ represents the inverse of the function, implying a reflection over the line $y = x$.
-
Graphing All Transforms
- For each transformed function, plot it on the same grid as the original function $f$ to observe the differences and transformations clearly.
The transformed functions are:
a) $-f(2x) - 3$
b) $2f(x - 4)$
c) $\frac{1}{2}f\left(-\frac{1}{2}x\right) - 6$
d) $f^{-1}$
More Information
Transformed functions help visualize how various alterations impact a function's graph. They demonstrate concepts like reflection, translation, and scaling, which are crucial in understanding function behavior.
Tips
- Mixing up reflection and translation: Ensure that you clearly differentiate between these transformations.
- Forgetting to adjust both x and y coordinates for changes: Remember that each transformation affects the graph's coordinates.
AI-generated content may contain errors. Please verify critical information