The characteristic equation for the matrix is \[ \begin{bmatrix} t & 3 \ 3 & -\epsilon \ 3 & \epsilon \end{bmatrix} = \lambda I \text{ where } I = \text{Identity matrix} \]
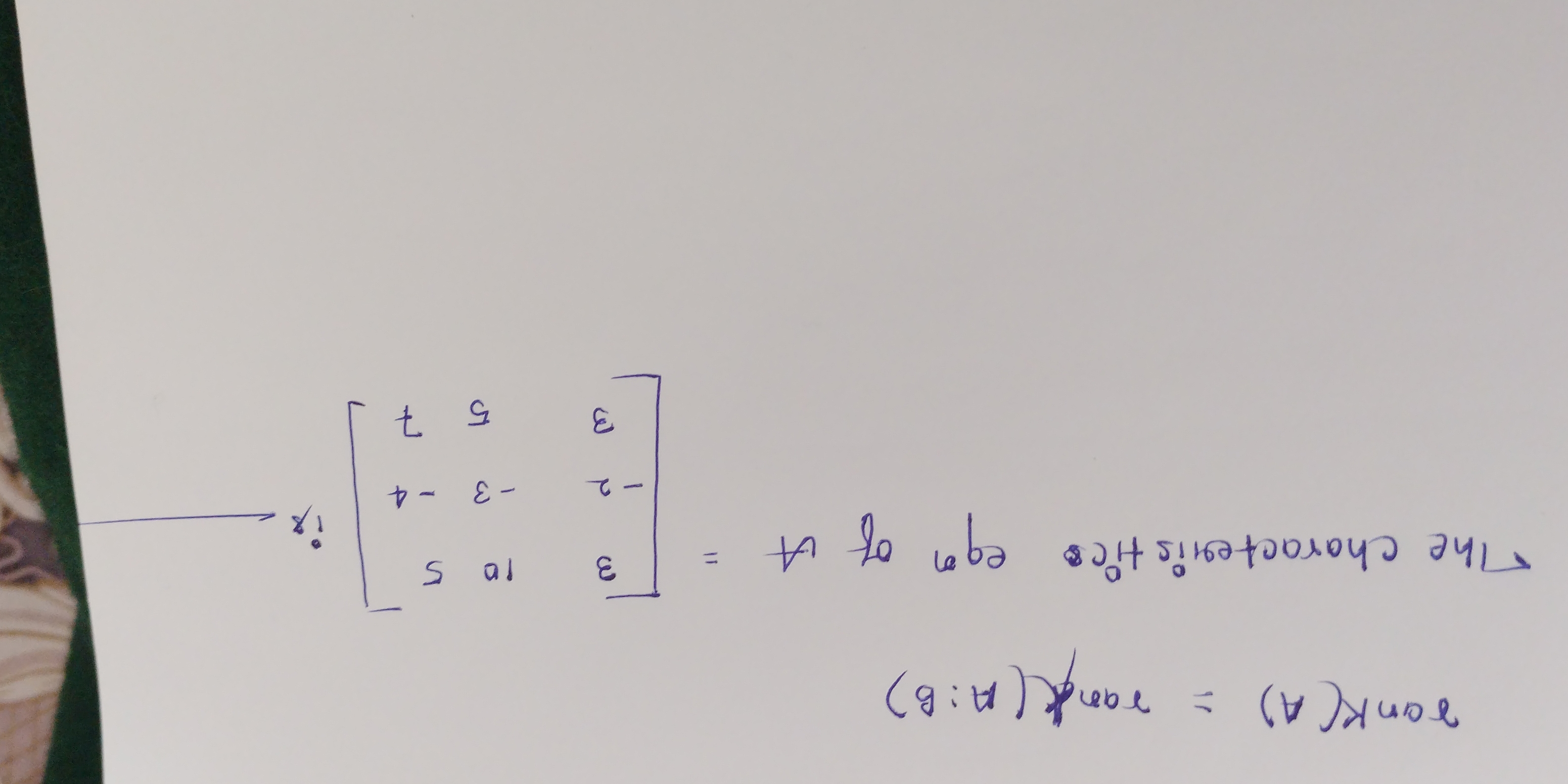
Understand the Problem
The question involves calculating the characteristic equation of a matrix typically represented in linear algebra. It appears to outline a mathematical problem regarding eigenvalues or determinants.
Answer
The characteristic equation is derived from $\text{det}(A - \lambda I) = 0$.
Answer for screen readers
The characteristic equation of the matrix $A$ is given by setting the determinant $\text{det}(A - \lambda I) = 0$, which results in a polynomial in terms of $\lambda$.
Steps to Solve
-
Identify the Matrix and the Values The given matrix appears to be: $$ A = \begin{bmatrix} t & 3 & 3 \ -e & 3 & -t \ s & 1 & e \end{bmatrix} $$ We need to find the characteristic polynomial, which is derived from the determinant of $A - \lambda I$, where $I$ is the identity matrix and $\lambda$ represents the eigenvalues.
-
Set Up the Characteristic Equation The characteristic equation is determined by: $$ \text{det}(A - \lambda I) = 0 $$ We represent $I$, the identity matrix, and adjust it according to $\lambda$: $$ A - \lambda I = \begin{bmatrix} t - \lambda & 3 & 3 \ -e & 3 - \lambda & -t \ s & 1 & e - \lambda \end{bmatrix} $$
-
Calculate the Determinant To find the determinant, we can use the formula for the determinant of a 3x3 matrix: If $$ B = \begin{bmatrix} a & b & c \ d & e & f \ g & h & i \end{bmatrix}, $$ then $$ \text{det}(B) = a(ei - fh) - b(di - fg) + c(dh - eg) $$
For our matrix $A - \lambda I$, we will expand the determinant using this formula.
- Expanding the Determinant Let’s denote the elements of $A - \lambda I$ as:
- $a = t - \lambda$
- $b = 3$
- $c = 3$
- $d = -e$
- $e = 3 - \lambda$
- $f = -t$
- $g = s$
- $h = 1$
- $i = e - \lambda$
We can substitute these into the determinant formula: $$ \text{det}(A - \lambda I) = (t - \lambda)((3 - \lambda)(e - \lambda) + t) - 3(-e(e - \lambda) + st) + 3(s(3 - \lambda) + e) $$
-
Simplify and Solve Now we need to simplify the expression obtained from the determinant and set it to zero to find the characteristic polynomial: $$ \text{det}(A - \lambda I) = 0 $$
-
Resulting Characteristic Polynomial After simplifying, the final form of the characteristic polynomial will yield the eigenvalues of the matrix.
The characteristic equation of the matrix $A$ is given by setting the determinant $\text{det}(A - \lambda I) = 0$, which results in a polynomial in terms of $\lambda$.
More Information
Finding the characteristic polynomial is crucial in linear algebra as it allows us to determine the eigenvalues of a matrix, which have applications in stability analysis, vibration analysis, and many other fields.
Tips
- Forgetting to include the identity matrix when calculating $A - \lambda I$.
- Miscalculating the determinant of the matrix.
- Not setting the determinant to zero to find the characteristic equation.
AI-generated content may contain errors. Please verify critical information