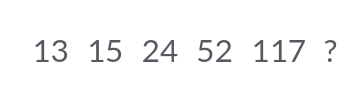
What is the next number in the sequence: 13, 15, 24, 52, 117?
Understand the Problem
The question is presenting a sequence of numbers (13, 15, 24, 52, 117) and asking for the next number in the sequence. The goal is to identify the pattern or rule governing the sequence to calculate the next term.
Answer
The next number in the sequence is $243$.
Answer for screen readers
The next number in the sequence is $243$.
Steps to Solve
- Identify the differences between consecutive terms
Calculate the difference between each term in the sequence:
- $15 - 13 = 2$
- $24 - 15 = 9$
- $52 - 24 = 28$
- $117 - 52 = 65$
This gives us the differences: 2, 9, 28, 65.
- Identify the differences of the differences
Now, calculate the differences of these differences:
- $9 - 2 = 7$
- $28 - 9 = 19$
- $65 - 28 = 37$
This gives us the second differences: 7, 19, 37.
- Identify the differences of the second differences
Next, calculate the differences of the second differences:
- $19 - 7 = 12$
- $37 - 19 = 18$
This gives us the third differences: 12, 18.
- Identify the next third difference
Assuming a linear pattern, the next third difference could be $18 + 6 = 24$.
- Calculate the next second difference
Now, add this to the last second difference:
$37 + 24 = 61$.
- Calculate the next first difference
Add this to the last first difference:
$65 + 61 = 126$.
- Calculate the next term in the sequence
Finally, add this to the last term:
$117 + 126 = 243$.
The next number in the sequence is $243$.
More Information
This sequence exhibits a pattern where each term follows a specific rule that involves consecutive differences. Recognizing the differences can help in predicting future terms in sequences.
Tips
- Not calculating the differences accurately can lead to incorrect conclusions. Always double-check your arithmetic.
- Assuming a pattern without checking the differences may lead to premature conclusions.
AI-generated content may contain errors. Please verify critical information